题目内容
15.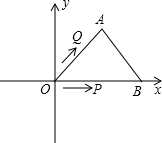 如图,等边三角形OAB的边长为6,P,Q是两个动点P沿OAB的路线运动,Q沿OBA路线运动P的速度是3,Q的速度是3,求A的坐标和P,Q相遇时的坐标.
如图,等边三角形OAB的边长为6,P,Q是两个动点P沿OAB的路线运动,Q沿OBA路线运动P的速度是3,Q的速度是3,求A的坐标和P,Q相遇时的坐标.
分析 过点A作AD⊥OB于点D,取AB的中点M,作ME⊥OB于点E,由△AOB是等边三角形可得出OD的长,根据勾股定理可求出AD的长,进而得出A点坐标;由点Q与点P的运动速度相同可知P、Q在AB的中点M处相遇,根据中点坐标公式求出点M的坐标即可.
解答  解:过点A作AD⊥OB于点D,取AB的中点M,作ME⊥OB于点E,
解:过点A作AD⊥OB于点D,取AB的中点M,作ME⊥OB于点E,
∵△AOB是边长为6的等边三角形,
∴OD=$\frac{1}{2}$OB=3,
∴AD=$\sqrt{{OA}^{2}-{OD}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴A(3,3$\sqrt{3}$);
∵点Q与点P的运动速度相同,
∴P、Q在AB的中点M处相遇,
∵B(6,0),
∴M($\frac{9}{2}$,$\frac{3\sqrt{3}}{2}$).
点评 本题考查的是等边三角形的性质,熟知等边三角形三线合一的性质是解答此题的关键.

练习册系列答案
相关题目
6.下列说法正确的是( )
| A. | 各边相等的多边形是正多边形 | |
| B. | 各角相等的多边形是正多边形 | |
| C. | 各边相等的圆内接多边形是正多边形 | |
| D. | 各角相等的圆内接多边形是正多边形 |
3.若a+b=0,则方程ax+b=0的解有( )
| A. | 只有一个解 | B. | 只有一个解或无解 | ||
| C. | 只有一个解或无数个解 | D. | 无解 |

 若点O为直线AB上一点,OC为射线,OE平分∠AOC,OF平分∠BOC.
若点O为直线AB上一点,OC为射线,OE平分∠AOC,OF平分∠BOC.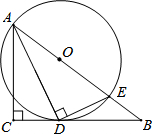 如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O
如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O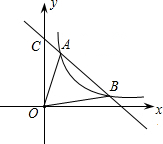 如图,一次函数y=-x+8和反比例函数y=$\frac{k}{x}$的图象在第一象限内有两个不同的公共点A(x1,y1)、B(x2,y2).
如图,一次函数y=-x+8和反比例函数y=$\frac{k}{x}$的图象在第一象限内有两个不同的公共点A(x1,y1)、B(x2,y2).