题目内容
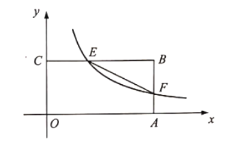
【题目】如图,平面直角坐标系中,![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象分别与线段
在第一象限内的图象分别与线段![]() 交于点
交于点![]() ,连接
,连接![]() ,如果点
,如果点![]() 关于
关于![]() 的对称点恰好落在
的对称点恰好落在![]() 边上,那么
边上,那么![]() 的值为______.
的值为______.
【答案】12
【解析】
根据A(8,0),B(8,4),C(0,4),可得矩形的长和宽,易知点F的横坐标,E的纵坐标,由反比例函数的关系式,可用含有k的代数式表示出点F的纵坐标和点E的横坐标,由三角形相似和对称,可求出AD的长,然后把问题转化到三角形ADF中,由勾股定理建立方程求出k的值.
过点E作EG⊥OA,垂足为G,设点B关于EF的对称点为D,连接DF、ED、BD,如图所示:
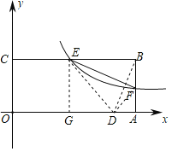
则△BEF≌△DEF,
∴BD=DF,BE=DE,∠FDE=∠FBE=90°,
∴∠EDG+∠ADF=∠ADF+∠AFD,
∴∠EDG=∠AFD,
∵∠EGD=∠DAF,
∴△ADF∽△GED,
∴![]() ,
,
∴AD:EG=BD:BE,
∵A(8,0),B(8,4),C(0,4),
∴AB=OC=EG=4,OA=BC=8,
∵E、F在反比例函数![]() 的图象上,
的图象上,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴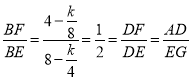 ,
,
∴![]()
在Rt△ADF中,由勾股定理:AD2+AF2=DF2
即:![]() , 解得:k=12,
, 解得:k=12,
故答案为12.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
【题目】已知抛物线y=-x2-2x+c与x轴的一个交点是(1,0).
(1)C的值为_______;
(2)选取适当的数据补填下表,并在平面直角坐标系内描点画出该抛物线的图像;
|
|
|
|
| |||
|
|
|
|
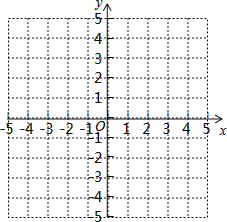
(3)根据所画图像,写出y>0时x的取值范围是_____.