题目内容
设直线(k+1)y﹢kx=1(k为正整数),与两坐标轴所围成的三角形的面积为Sk(k=1,2,3,…,2013),则S1+S2+…+S2013的值为________.
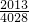
分析:当x=0时,y=
 ,当y=0时,x=
,当y=0时,x= ,所以面积S=
,所以面积S= •
• •
• =
= (
(  -
- ),根据规律代入数据可求出值.
),根据规律代入数据可求出值.解答:当x=0时,y=
 ,当y=0时,x=
,当y=0时,x= ,
,面积S=
 •
• •
• =
= (
(  -
- ),
),∴S1+S2+…+S2013=
 (
( -
- +
+
 +…+
+…+ -
-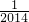 )=
)= (1-
(1-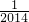 )=
)=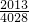 ,
,故答案为:
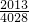 .
.点评:本题主要考查了一次函数图象上的点的坐标特点,考查找规律的能力,关键能看分式的特点.

练习册系列答案
相关题目
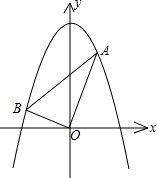 接OA,OB,OA⊥OB.
接OA,OB,OA⊥OB.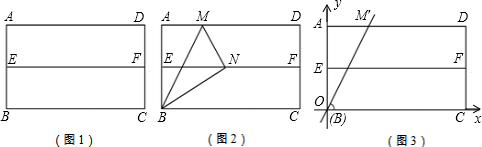
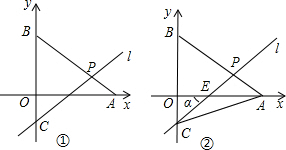 AB交于点P.
AB交于点P.
 (圆心P在x轴上),抛物线y=
(圆心P在x轴上),抛物线y=