题目内容
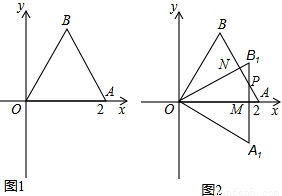
等边△AOB在平面直角坐标系中(图1),已知点A(2,0),将△AOB绕着点O顺时针方向旋转的角度为α(0°<α<360°)得到△OA1B1
(1)直接写出点B的坐标
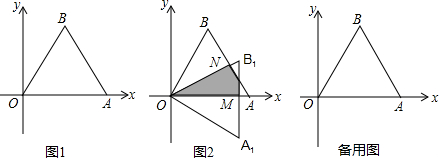
(2)当α=30°时,△AOB与△OA1B1重合部分(图2的阴影部分)的面积是
(3)当点A1B1的纵坐标相同时,α的值为
(4)当60°<α<180°时,设直线A1B1与直线BA相交于点P,若PA、PB1的长是方程x2-mx+m=0的两个实数根,求此时点P的坐标.

(1)直接写出点B的坐标
(1,
)
| 3 |
(1,
)
;| 3 |
(2)当α=30°时,△AOB与△OA1B1重合部分(图2的阴影部分)的面积是
6-3
| 3 |
6-3
;| 3 |
(3)当点A1B1的纵坐标相同时,α的值为
120°或300°
120°或300°
;(4)当60°<α<180°时,设直线A1B1与直线BA相交于点P,若PA、PB1的长是方程x2-mx+m=0的两个实数根,求此时点P的坐标.
分析:(1)根据A点坐标可知,正三角形的边长是2,过B作x轴的垂线,根据三角函数即可求得;
(2)阴影部分的面积=S△OAN-S△QAM,而这两个三角形的面积很容易得到;
(3)当A1,B1的纵坐标相同时,A1B1∥x轴,a1=120°或a2=300°;
(4)可以证明PA=PB1,即方程x2-mx+m=0的两个相等实数根,根据根的判别式即可求得m的值,从而求得PA,PB1的长,得到P的坐标.
(2)阴影部分的面积=S△OAN-S△QAM,而这两个三角形的面积很容易得到;
(3)当A1,B1的纵坐标相同时,A1B1∥x轴,a1=120°或a2=300°;
(4)可以证明PA=PB1,即方程x2-mx+m=0的两个相等实数根,根据根的判别式即可求得m的值,从而求得PA,PB1的长,得到P的坐标.
解答:解:(1)B的坐标是(1,
);
(2)图2中的阴影部分的面积=S△OAN-S△QAM=
×1×
-
×
×(2-
)2=6-3
;
(3)∵当A1,B1的纵坐标相同时,A1B1∥x轴,
∴a1=120°或a2=300°;
(4)连接AB1,
∵OA=OB1=2,
∴∠OAB1=∠0B1A,
∴∠PB1G=∠B1AH,
又∵∠PAB1=180°-60°-∠B1AH=120°-∠B1AH,
∠PB1A=180°-60°-∠AB1G=120°-∠AB1G,
∴∠PAB1=∠PB1A,
∴PA=PB1(6分)
∴方程x2-mx+m=0的两个相等实数根,
∴△=(-m)2-4m=0,
解得:m1=0(舍去),m2=4,
方程为:x2-4x+4=0,
解得:x1=x2=2,
∴PA=PB1=2,
在直角△APM中,PM=AP•sin60°=2×
=
,
AM=AP•cos60°=1,则OM=OA-AM=3-1=2.
∴P点坐标为(3,-
).
故答案为:(1)(1,
);(2)6-3
;(3)120°或300°
| 3 |
(2)图2中的阴影部分的面积=S△OAN-S△QAM=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
(3)∵当A1,B1的纵坐标相同时,A1B1∥x轴,
∴a1=120°或a2=300°;
(4)连接AB1,
∵OA=OB1=2,

∴∠OAB1=∠0B1A,
∴∠PB1G=∠B1AH,
又∵∠PAB1=180°-60°-∠B1AH=120°-∠B1AH,
∠PB1A=180°-60°-∠AB1G=120°-∠AB1G,
∴∠PAB1=∠PB1A,
∴PA=PB1(6分)
∴方程x2-mx+m=0的两个相等实数根,
∴△=(-m)2-4m=0,
解得:m1=0(舍去),m2=4,
方程为:x2-4x+4=0,
解得:x1=x2=2,
∴PA=PB1=2,
在直角△APM中,PM=AP•sin60°=2×
| ||
| 2 |
| 3 |
AM=AP•cos60°=1,则OM=OA-AM=3-1=2.
∴P点坐标为(3,-
| 3 |
故答案为:(1)(1,
| 3 |
| 3 |
点评:本题综合运用了平行于x轴的点的坐标的关系,涉及的知识有:坐标与图形性质,锐角三角函数定义,一元二次方程的根的判别式,题目难度较大.

练习册系列答案
相关题目
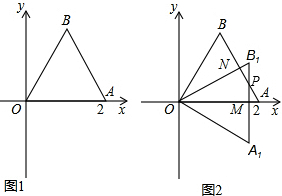
 如图,将边长为8的等边△AOB置于平面直角坐标系中,点A在x轴正半轴上,过点O作OC⊥AB于点C,将△OAC绕着原点O逆时针旋转60°得到△OBD,这时,点D恰好落在y轴上.若动点E从原点O出发,沿线段OC向终点C运动,动点F从点D出发,沿线段DO向终点O运动,两点同时出发,速度均为每秒1个单位长度.设运动的时间为t秒.
如图,将边长为8的等边△AOB置于平面直角坐标系中,点A在x轴正半轴上,过点O作OC⊥AB于点C,将△OAC绕着原点O逆时针旋转60°得到△OBD,这时,点D恰好落在y轴上.若动点E从原点O出发,沿线段OC向终点C运动,动点F从点D出发,沿线段DO向终点O运动,两点同时出发,速度均为每秒1个单位长度.设运动的时间为t秒.