题目内容
已知半径为1的圆的圆心是坐标原点，半径为3的圆的圆心坐标是（
，1），则两圆的位置关系是
- A.外切
- B.内切
- C.相交
- D.外离
B
分析：先根据两点间的距离公式计算出圆心距=2，再计算出半径之差=2，然后根据圆与圆的位置关系的判定方法求解．
解答：圆心距=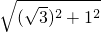
=2，
而半径之差=3-1=2，
所以圆心距等于两圆的半径之差，
所以两圆内切．
故选B．
点评：本题考查了圆和圆的位置关系：设两圆的圆心距、半径分别为d、R、r，则两圆外离?d＞R+r；两圆外切?d=R+r；两圆相交?R-r＜d＜R+r（R≥r）；两圆内切?d=R-r（R＞r）；两圆内含?d＜R-r（R＞r）．
分析：先根据两点间的距离公式计算出圆心距=2，再计算出半径之差=2，然后根据圆与圆的位置关系的判定方法求解．
解答：圆心距=
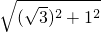=2，而半径之差=3-1=2，
所以圆心距等于两圆的半径之差，
所以两圆内切．
故选B．
点评：本题考查了圆和圆的位置关系：设两圆的圆心距、半径分别为d、R、r，则两圆外离?d＞R+r；两圆外切?d=R+r；两圆相交?R-r＜d＜R+r（R≥r）；两圆内切?d=R-r（R＞r）；两圆内含?d＜R-r（R＞r）．
练习册系列答案
相关题目
（2011•成华区二模）如图，已知半径为R的⊙O1的直径AB和弦CD交于点M，点A为
，1)，则两圆的位置关系是
,1 ),则两圆的位置关系是：（ ）