题目内容
10.已知关于x的方程mx2+2x+3=0有实数根,那么实数m的取值范围为m≤$\frac{1}{3}$.分析 从m=0和m≠0两种情况进行分析,运用一元二次方程根的判别式列出不等式,解不等式即可.
解答 解:当m=0时,方程可化为2x+3=0,x=-$\frac{3}{2}$,有实根,
当m≠0时,方程有实数根,则22-12m≥0,
解得m≤$\frac{1}{3}$.
故答案为:m≤$\frac{1}{3}$.
点评 本题考查的是一元二次方程根的判别式,掌握△>0?方程有两个不相等的实数根;△=0?方程有两个相等的实数根;△<0?方程没有实数根是解题的关键,注意分情况讨论思想的应用.

练习册系列答案
相关题目
1.下列命题是真命题的是( )
| A. | 任何数的0次幂都等于1 | |
| B. | 顺次连接菱形四边中点的线段组成的四边形是正方形 | |
| C. | 图形的旋转和平移会改变图形的形状和大小 | |
| D. | 角平分线上的点到角两边的距离相等 |
5.既不是正数,也不是负数的数是( )
| A. | 1 | B. | 0 | C. | π | D. | $\frac{1}{3}$ |
 已知:如图所示,AB为⊙O的直径,C是⊙O外一点,BC交⊙O于点E,AC交⊙O于点D,∠D0E=60°,求∠C的度数.
已知:如图所示,AB为⊙O的直径,C是⊙O外一点,BC交⊙O于点E,AC交⊙O于点D,∠D0E=60°,求∠C的度数.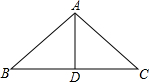 如图所示是一个等腰三角形形状的梁架,腰AB=5米,底边BC=8米,AD是底边BC上的高,则$\frac{BD}{AB}$=$\frac{4}{5}$,$\frac{AD}{AB}$=$\frac{3}{5}$.
如图所示是一个等腰三角形形状的梁架,腰AB=5米,底边BC=8米,AD是底边BC上的高,则$\frac{BD}{AB}$=$\frac{4}{5}$,$\frac{AD}{AB}$=$\frac{3}{5}$.