题目内容
20.如图所示,点A为半圆O直径MN所在直线上一点,射线AB垂直于MN,垂足为A,半圆绕M点顺时针转动,转过的角度记作a;设半圆O的半径为R,AM的长度为m,回答下列问题:探究:(1)若R=2,m=1,如图1,当旋转30°时,圆心O′到射线AB的距离是$\sqrt{3}$+1;如图2,当a=60°时,半圆O与射线AB相切;
(2)如图3,在(1)的条件下,为了使得半圆O转动30°即能与射线AB相切,在保持线段AM长度不变的条件下,调整半径R的大小,请你求出满足要求的R,并说明理由.
(3)发现:(3)如图4,在0°<α<90°时,为了对任意旋转角都保证半圆O与射线AB能够相切,小明探究了cosα与R、m两个量的关系,请你帮助他直接写出这个关系;cosα=$\frac{R-m}{R}$(用含有R、m的代数式表示)
拓展:(4)如图5,若R=m,当半圆弧线与射线AB有两个交点时,α的取值范围是90°<α≤120°,并求出在这个变化过程中阴影部分(弓形)面积的最大值(用m表示)

分析 (1)如图1中,作O′E⊥AB于E,MF⊥O′E于F.则四边形AMFE是矩形,EF=AM=1.如图2中,设切点为F,连接O′F,作O′E⊥OA于E,则四边形O′EAF是矩形,在Rt△O′EM中,由sinα=$\frac{O′E}{O′M}$=$\frac{1}{2}$,推出α=60°.
(2)设切点为P,连接O′P,作MQ⊥O′P,则四边形APQM是矩形.列出方程即可解决问题.
(3)设切点为P,连接O′P,作MQ⊥O′P,则四边形APQM是矩形.列出方程即可解决问题、
(4)当半圆与射线AB相切时,之后开始出现两个交点,此时α=90°;当N′落在AB上时,为半圆与AB有两个交点的最后时刻,此时∵MN′=2AM,所以∠AMN′=60°,所以,α=120°因此,当半圆弧线与射线AB有两个交点时,α的取值范围是:90°<α≤120°.当N′落在AB上时,阴影部分面积最大,求出此时的面积即可.
解答 解:(1)如图1中,作O′E⊥AB于E,MF⊥O′E于F.则四边形AMFE是矩形,EF=AM=1.想办法求出O′E的长即可.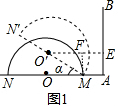
在Rt△MFO′中,∵∠MO$′\\;F$F=30°,MO′=2,
∴O′F=O′M•cos30°=$\sqrt{3}$,O′E=$\sqrt{3}$+1,
∴点O′到AB的距离为$\sqrt{3}$+1.
如图2中,设切点为F,连接O′F,作O′E⊥OA于E,则四边形O′EAF是矩形,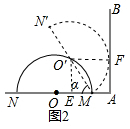
∴AE=O′F=2,
∵AM=1,
∴EM=1,
在Rt△O′EM中,sinα=$\frac{O′E}{O′M}$=$\frac{1}{2}$,
∴α=60°
故答案为$\sqrt{3}$+1,60°.
(2)设切点为P,连接O′P,作MQ⊥O′P,则四边形APQM是矩形.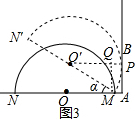
∵O′P=R,
∴R=$\frac{\sqrt{3}}{2}$R+1,
∴R=4+2$\sqrt{3}$.
(3)设切点为P,连接O′P,作MQ⊥O′P,则四边形APQM是矩形.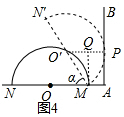
在Rt△O′QM中,O′Q=R•cosα,QP=m,
∵O′P=R,
∴R•cosα+m=R,
∴cosα=$\frac{R-m}{R}$.
故答案为$\frac{R-m}{R}$.
(4)如图5中,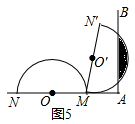
当半圆与射线AB相切时,之后开始出现两个交点,此时α=90°;当N′落在AB上时,为半圆与AB有两个交点的最后时刻,此时∵MN′=2AM,所以∠AMN′=60°,所以,α=120°因此,当半圆弧线与射线AB有两个交点时,α的取值范围是:90°<α≤120°
故答案为90°<α≤120°;
当N′落在AB上时,阴影部分面积最大,
所以S═$\frac{120•π•{m}^{2}}{360}$-$\frac{1}{2}$•$\sqrt{3}$m•$\frac{1}{2}$m=$\frac{π{m}^{2}}{3}$-$\frac{\sqrt{3}}{4}$m2.
点评 本题考查圆综合题、旋转变换、切线的判定和性质、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形或特殊四边形解决问题,所以中考压轴题.

| A. | 有两个不相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
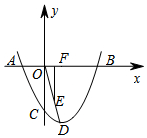 如图,一抛物线经过点A(-2,0),B(6,0),C(0,-3),D为抛物线的顶点,过OD的中点E,作EF⊥x轴于点F,G为x轴上一动点,M为抛物线上一动点,N为直线EF上一动点,当以F、G、M、N为顶点的四边形是正方形时,点G的坐标为(4-2$\sqrt{6}$,0)、(-4,0)、(4+2$\sqrt{6}$,0)或(4,0).
如图,一抛物线经过点A(-2,0),B(6,0),C(0,-3),D为抛物线的顶点,过OD的中点E,作EF⊥x轴于点F,G为x轴上一动点,M为抛物线上一动点,N为直线EF上一动点,当以F、G、M、N为顶点的四边形是正方形时,点G的坐标为(4-2$\sqrt{6}$,0)、(-4,0)、(4+2$\sqrt{6}$,0)或(4,0).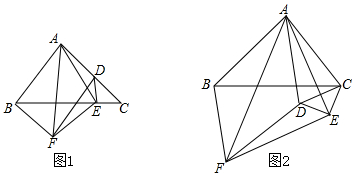
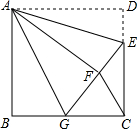 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,FC,下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,FC,下列结论: