题目内容
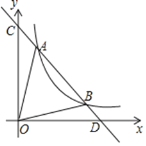
如图,一次函数
 (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.
(1)求反比例函数的解析式;
(2)根据图象直接写出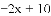
 的x的取值范围;
的x的取值范围;
(3)求
【答案】(1)y= ;(2)
;(2) 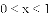
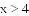
【解析】(1)把B(4,n)两点分别代入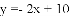
(2)观察函数图象得到当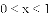
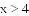
(3)求得直线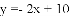
(1)将
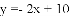
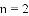
得反比例函数的关系式是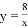 .
.
(2)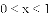
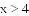
(3)
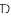
分别过点A、B两点作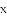
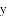
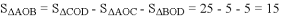 .
.
点睛:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式以及观察图象的能力.
【题型】解答题
【结束】
25
探索发现: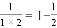 ;
;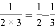 ;
;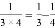 …根据你发现的规律,回答下列问题
…根据你发现的规律,回答下列问题
(1)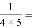 ,
,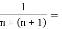 ;
;
(2)利用你发现的规律计算: ;
;
(3)灵活利用规律解方程:
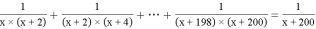
练习册系列答案
相关题目


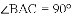
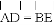 .
.