题目内容
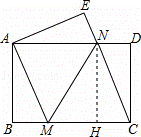
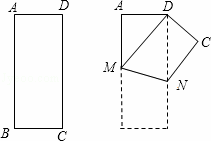
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:1,且CD=4,求线段MN的长.
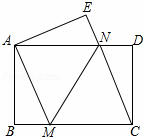
(1)证明:由折叠的性质可得:∠ANM=∠CNM.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ANM=∠CMN,
∴∠CMN=∠CNM,
∴CM=CN;
(2)解:过点N作NH⊥BC于点H,则四边形NHCD是矩形.
∴HC=DN,NH=DC.
∵△CMN的面积与△CDN的面积比为3:1,
∴MC=3ND=3HC.
∴MH=2HC.
设DN=x,则HC=x,MH=2x,
∴CM=3x=CN,
在Rt△CDN中,CD=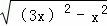 =2
=2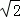 x=4,
x=4,
∴x=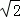 .
.
∴MH=2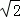 .
.
在Rt△MNH中,MN=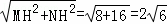 .
.
点评: 此题考查了矩形的性质、折叠的性质、勾股定理以及三角形的面积.此题难度适中,注意掌握辅助线的作法,掌握数形结合思想与方程思想的应用.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
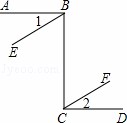


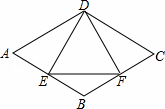
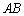 ,
,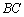 ,
, 分别与⊙
分别与⊙ 相切于
相切于 ,
, ,
, 三点,且
三点,且 ,
, .
. 的度数;
的度数;
 (Ⅱ)如图②,延长
(Ⅱ)如图②,延长 交⊙
交⊙ ,过点
,过点 ∥
∥ ,当
,当 ,
, 时,求⊙
时,求⊙