题目内容
如图,将矩形ABCD沿MN折叠,使点B与点D重合.
(1)求证:DM=DN;
(2)当AB和AD满足什么数量关系时,△DMN是等边三角形?并说明你的理由.
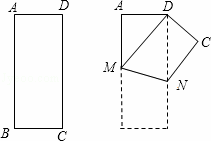
(1)证明:由题意知∠1=∠2,
又AB∥CD,得∠1=∠3,
则∠2=∠3.
故DM=DN;
(2)解:当AB= AD时,△DMN是等边三角形.
AD时,△DMN是等边三角形.
证明:连接BD.
∵∠A=90°,AB= AD,
AD,
∴tan∠ABD=
 =
= ,
,
∴∠ABD=30°.
∵BM=MD,
∴∠ABD=∠MDB=30°,
∴∠BMD=120°.
∴∠1=∠2=60°.
又DM=DN,
∴△DMN是等边三角形.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 >B班的方差
>B班的方差 ,得出结论是:B班的成绩比A班的好.其中正确的是 (只填序号)
,得出结论是:B班的成绩比A班的好.其中正确的是 (只填序号)
 B.
B. C.
C.  D.
D. 

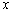 轴的直线
轴的直线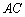 分别交函数
分别交函数 (
( (
(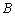 ,
,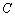 两点,过点
两点,过点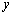 轴的平行线交
轴的平行线交 的图象于点
的图象于点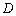 ,直线
,直线 ∥
∥ 的图象于点
的图象于点 ,则
,则 .
.