题目内容
13.甲、乙两人5次射击命中的环数分别为,甲:7,9,8,6,10;乙:7,8,9,8,8;$\overline{x_甲}=\overline{x_乙}$=8,则这两人5次射击命中的环数的方差S甲2>S乙2(填“>”“<”或“=”).分析 分别根据方差公式计算出甲、乙两人的方差,再比较大小.
解答 解:∵$\overline{x_甲}=\overline{x_乙}$=8,
∴${S}_{甲}^{2}$=$\frac{1}{5}$[(7-8)2+(9-8)2+(8-8)2+(6-8)2+(10-8)2]=$\frac{1}{5}$(1+1+0+4+4)=2,
${S}_{乙}^{2}$=$\frac{1}{5}$[(7-8)2+(8-8)2+(9-8)2+(8-8)2+(8-8)2]=$\frac{1}{5}$(1+0+1+0+0)=0.4,
∴${S}_{甲}^{2}$>${S}_{乙}^{2}$,
故答案为:>.
点评 本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.

练习册系列答案
相关题目
5.用反证法证明“若a>b>0,则a2>b2”时,应假设( )
| A. | a2≤b2 | B. | a2≥b2 | C. | a2>b2 | D. | a2<b2 |
2.下列计算正确的是( )
| A. | m3•m3=2m3 | B. | m4÷m2=2 | C. | (-mn)4=m4n4 | D. | (2m3)3=6m6 |
3.下列各式中,计算正确的是( )
| A. | $\sqrt{(-4)^{2}}$=4 | B. | $\sqrt{25}$=±5 | C. | $\root{3}{(-1)^{3}}$=1 | D. | $\root{3}{125}$=±5 |
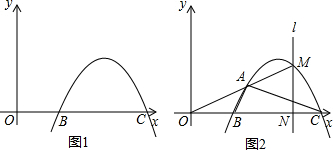
 如图,直线y=-x+3分别交x轴于点B、交y轴于点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
如图,直线y=-x+3分别交x轴于点B、交y轴于点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2. 已知,如图,在△ABC中,已知AB=AC=5cm,BC=6cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线QD从点C出发,沿CB方向匀速运动,速度为1cm/s,且QD⊥BC,与AC,BC分别交于点D,Q;当直线QD停止运动时,点P也停止运动.连接PQ,设运动时间为t(0<t<3)s.解答下列问题:
已知,如图,在△ABC中,已知AB=AC=5cm,BC=6cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线QD从点C出发,沿CB方向匀速运动,速度为1cm/s,且QD⊥BC,与AC,BC分别交于点D,Q;当直线QD停止运动时,点P也停止运动.连接PQ,设运动时间为t(0<t<3)s.解答下列问题: