题目内容
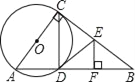
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
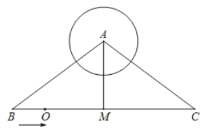
的中点.![]() 的半径为3,动点
的半径为3,动点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒1个单位的速度向点
方向以每秒1个单位的速度向点![]() 运动,设运动时间为
运动,设运动时间为![]() 秒.
秒.
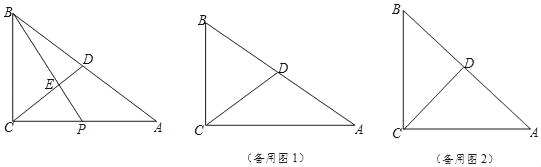
(1)当以![]() 为半径的
为半径的![]() 与
与![]() 相切时,求
相切时,求![]() 的值;
的值;
(2)探究:在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与直线
与直线![]() 相切,且与
相切,且与![]() 相外切?若存在,求出此时
相外切?若存在,求出此时![]() 的值及相应的
的值及相应的![]() 的半径;若不存在,请说明理由.
的半径;若不存在,请说明理由.
【答案】(1)当![]() 或
或![]() 时,
时,![]() 与
与![]() 相切;(2)存在,当
相切;(2)存在,当![]() 或
或![]() 时,
时,![]() ,
,![]() 与直线
与直线![]() 相切并且与
相切并且与![]() 相外切,理由见解析.
相外切,理由见解析.
【解析】
(1)在△ABC中,根据AB=AC,M为BC中点得到AM⊥BC,在Rt△ABM中,AB=10,BM=8得到AM=6.然后分当⊙O与⊙A相外切与当⊙O与⊙A相内切两种情况求得t值即可;
(2)分当点O在BM上运动时(0<t≤8)和当点O在MC上运动时(8<t≤16)两种情况求得t值即可.
解:(1)在![]() 中,∵
中,∵![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() .
.
当![]() 与
与![]() 相外切,
相外切,
可得![]() 解得
解得![]() .
.
当![]() 与
与![]() 相内切,
相内切,
可得![]() 解得
解得![]() ,
,
∴当![]() 或
或![]() 时,
时,![]() 与
与![]() 相切.
相切.
(2)存在.
当点![]() 在
在![]() 上运动时(
上运动时(![]() ),
),
可得![]() 解得
解得![]() ,
,
此时半径![]() .
.
当点![]() 在
在![]() 上运动时(
上运动时(![]() )
)
可得![]() 解得
解得![]() .
.
此时半径![]() .
.
当![]() 或
或![]() 时,
时,![]() ,
,![]() 与直线
与直线![]() 相切并且与
相切并且与![]() 相外切.
相外切.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目