Question

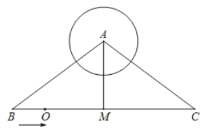
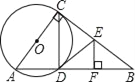
【题目】已知：如图△ABC中，∠ACB＝90°，以AC为直径的⊙O交AB于D，过D作⊙O的切线交BC于点E，EF⊥AB，垂足为F．

(1)求证：DE＝BC；

(2)若AC＝6，BC＝8，求S△ACD：S△EDF的值．

Answer 1

【答案】(1)证明见解析；(2)S△ACD：S△EDF＝9：4.

【解析】

（1）根据题意可知：EC、ED均是圆O的切线，根据切线长定理可得出EC＝DE，∠ECD＝∠EDC；根据等角的余角相等，可得出∠EDB＝∠B，因此DE＝BE，由此可得出DE＝EC＝BE，由此可得证；
（2）由（1）知：DE＝BE，因此DF＝BF，根据等高的三角形面积比等于底边比可得出△EDF的面积是△EDB的面积的一半，同理可得出△EDB的面积是△CDB的面积的一半，因此△EDF的面积是△CDB的面积的四分之一．那么本题只需得出△ADC和△CDB的面积比即可，即得出AD：BD的值即可．

(1)∵EC、ED都是⊙O的切线，

∴EC＝ED，∠ECD＝∠EDC．

∵∠EDC＋∠EDB＝90°，∠ECD＋∠B＝90°，

∴∠EDB＝∠B．

∴ED＝BE．

∴DE＝BE＝EC．

∴DE＝BC．

(2)在Rt△ABC中，AC＝6，BC＝8，则AB＝10，

根据射影定理可得：

AD＝AC2÷AB＝3.6，

BD＝BC2÷AB＝6.4，

∴S△ACD：S△BCD＝AD：BD＝9：16，

∵ED＝EB，EF⊥BD，

∴S△EDF＝S△EBD，

同理可得S△EBD＝S△BCD，

∴S△EDF＝S△BCD，

∴S△ACD：S△EDF＝．