题目内容
8．写出一个以$1+\sqrt{7}$与$1-\sqrt{7}$为根的一元二次方程x2-2x-6=0．分析 先计算出$1+\sqrt{7}$与$1-\sqrt{7}$的和与积，然后根据根与系数的关系写出满足条件的一元二次方程．
解答 解：∵1+$\sqrt{7}$+1-$\sqrt{7}$=2，（1+$\sqrt{7}$）（1-$\sqrt{7}$）=12-（$\sqrt{7}$）2=-6，
∴以$1+\sqrt{7}$与$1-\sqrt{7}$为根的一元二次方程可为x2-2x-6=0．
故答案为x2-2x-6=0．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
相关题目
18．下列命题是真命题的是（ ）
| A． | 有一个角相等的两个等腰三角形相似 | |
| B． | 两边对应成比例且有一个角相等的两个三角形相似 | |
| C． | 四个内角都对应相等的两个四边形相似 | |
| D． | 斜边和一条直角边对应成比例的两个直角三角形相似 |
16．
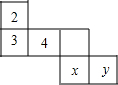如图是一个正方体的表面展开图，相对面上两个数互为相反数，则x+y=（ ）
如图是一个正方体的表面展开图，相对面上两个数互为相反数，则x+y=（ ）| A． | 6 | B． | -5 | C． | 7 | D． | -6 |
3．袋子中装有2个红球、3个白球和3个黄球，这些球除颜色外无其他差别，从袋子中随机摸出一个球，是白球的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{3}{8}$ | C． | $\frac{5}{8}$ | D． | $\frac{3}{4}$ |
如图，P为△ABC中BC边的延长线上一点，∠A=48°，∠B=64，则∠ACP=112°．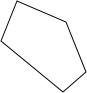
用三种不同的方法把图中的五边形分割成三角形，每种方法各分割成多少个三角形？