题目内容
若方程-x2+px+q=0的一个根大于1，另一个根小于1，则p+q的取值范围为 ．
考点：抛物线与x轴的交点
专题：
分析：先根据方程-x2+px+q=0的一个根大于1，另一个根小于1可知，当x=1时，y＞0，由此可得出结论．
解答：解：令y=-x2+px+q，
∵方程-x2+px+q=0的一个根大于1，另一个根小于1，
∴当x=1时，y＞0，即-12+p+q＞0，解得p+q＞1．
故答案为：p+q＞1．
∵方程-x2+px+q=0的一个根大于1，另一个根小于1，
∴当x=1时，y＞0，即-12+p+q＞0，解得p+q＞1．
故答案为：p+q＞1．
点评：本题考查的是抛物线与x轴的交点，根据题意得出当x=1时，y＞0是解答此题的关键．
练习册系列答案
相关题目
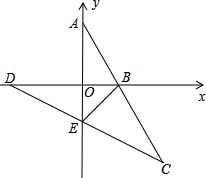已知如图在平面直角坐标系中点A（0，2），点B（1，0），连接AB并延长至C，使BC=AB，点D（-4，0），DC与y轴交于点E，连接BE，试着判断∠AED与∠BEC的数量关系，并说明理由．