题目内容
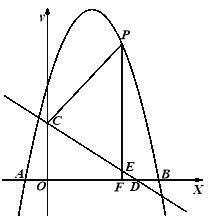
【题目】如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=![]() (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(1)求该双曲线所表示的函数解析式;
(2)求等边△AEF的边长.

【答案】(1)y=![]() ;(2)等边△AEF的边长是4
;(2)等边△AEF的边长是4![]() ﹣8.
﹣8.
【解析】试题分析:(1)过点C作CG⊥OA于点G,根据等边三角形的性质求出![]() 的长度,从而得到点
的长度,从而得到点![]() 的坐标,再利用 待定系数法求反比例函数解析式列式计算即可得解;
的坐标,再利用 待定系数法求反比例函数解析式列式计算即可得解;
(2)过点D作DH⊥AF于点H,设AH=a,,根据等边三角形的性质表示出![]() 的长度,然后表示出点
的长度,然后表示出点![]() 的坐标,再把点
的坐标,再把点![]() 的坐标代入反比例函数解析式,解方程得到
的坐标代入反比例函数解析式,解方程得到![]() 的值,从而得解.
的值,从而得解.
试题解析:(1)过点C作CG⊥OA于点G,

∵点C是等边△OAB的边OB的中点,
![]()
![]()
∴点C的坐标是![]()
由![]() 得:
得: ![]()
∴该双曲线所表示的函数解析式为![]()
(2)过点D作DH⊥AF于点H,设AH=a,则![]()
∴点D的坐标为![]()
∵点D是双曲线![]() 上的点,
上的点,
由![]() ,得
,得![]()
即: ![]()
解得: ![]() (舍去),
(舍去),
![]()
∴等边△AEF的边长是2AD=![]()

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目