题目内容
18．某校10名学生参加“心理健康”知识测试，他们得分情况如下表：| 人数 | 2 | 3 | 4 | 1 |
| 分数 | 80 | 85 | 90 | 95 |
| A． | 95和85 | B． | 90和85 | C． | 90和87.5 | D． | 85和87.5 |
分析 找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数；众数是一组数据中出现次数最多的数据，可得答案．
解答 解：在这一组数据中9是出现次数最多的，故众数是90；
排序后处于中间位置的那个数是85，90，那么由中位数的定义可知，这组数据的中位数是$\frac{85+90}{2}$=87.5；
故选：C．
点评 本题为统计题，考查极差、众数与中位数的意义．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数），叫做这组数据的中位数．如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．
练习册系列答案
相关题目
8．
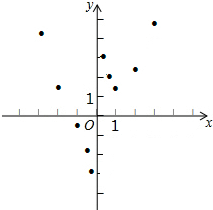有这样一个问题：探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质．
小东根据学习函数的经验，对函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质进行了探究．
下面是小东的探究过程，请补充完整：
（1）函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值．
求m的值；
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）进一步探究发现，该函数图象在第一象限内的最低点的坐标是（1，$\frac{3}{2}$），结合函数的图象，写出该函数的其它性质（一条即可）该函数没有最大值．
有这样一个问题：探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质．小东根据学习函数的经验，对函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质进行了探究．
下面是小东的探究过程，请补充完整：
（1）函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值．
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{25}{6}$ | $\frac{3}{2}$ | -$\frac{1}{2}$ | -$\frac{15}{8}$ | -$\frac{53}{18}$ | $\frac{55}{18}$ | $\frac{17}{8}$ | $\frac{3}{2}$ | $\frac{5}{2}$ | m | … |
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）进一步探究发现，该函数图象在第一象限内的最低点的坐标是（1，$\frac{3}{2}$），结合函数的图象，写出该函数的其它性质（一条即可）该函数没有最大值．
如图，在△ABC中，AB=8，点D、E分别是BC、CA的中点，连接DE，则DE=4．
如图，两幢建筑物AB和CD，AB⊥BD，CD⊥BD，AB=15m，CD=20m，AB和CD之间有一景观池，小南在A点测得池中喷泉处E点的俯角为42°，在C点测得E点的俯角为45°（点B、E、D在同一直线上），求两幢建筑物之间的距离BD（结果精确到0.1m）．（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）
在平行四边形ABCD中，E为BC边上的一点．连结AE．