Question

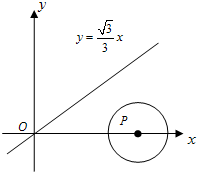圆P的半径为1，圆心P从x轴正半轴向负半轴运动，P在正半轴速度为1/s，在负半轴运动速度为0.5/s，问：圆P与直线相交的时间为多少？

Answer 1

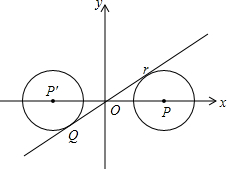解：设⊙P向左移动的过程中与直线相切于Q点，
∵∠TOP=30°
∴在Rt△TOP中，OP=2TP=2，
∴此时P的坐标有（2，0），同样在x的负半轴P′的坐际为（-2，0）．
∴在两点运动之间圆与直线保持相交状态，相交时间．
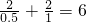分析：先根据圆P与直线相切求出∠TOP的度数，在Rt△TOP中可得出OP的长，进而得出点P及点P′的坐标，再由P在正半轴速度为1/s，在负半轴运动速度为0.5/s即可得出结论．
点评：本题考查的是一次函数综合题，先根据题意得出点P及点P′的坐标是解答此题的关键．