题目内容
20.若方程组$\left\{\begin{array}{l}{2x+3y=1}\\{(k-1)x+(k+1)y=4}\end{array}\right.$的解x与y相等,则k的值为10.分析 将2x+3y=1与x=y组成方程组,求出x、y的值,再代入(k-1)x+(k+1)y=4即可求出k的值.
解答 解:由题意得$\left\{\begin{array}{l}{2x+3y=1}\\{x=y}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{1}{5}}\\{y=\frac{1}{5}}\end{array}\right.$,
把x=$\frac{1}{5}$,y=$\frac{1}{5}$代入(k-1)x+(k+1)y=4得,
$\frac{1}{5}$(k-1)+$\frac{1}{5}$(k+1)=4,
解得k=10,
故答案为10.
点评 本题考查了二元一次方程组的解,求出x与y的值是解题的关键.

练习册系列答案
相关题目
10.平行四边形的一边长是6,则它的对角线长可能是( )
| A. | 4和8 | B. | 2和12 | C. | 4和6 | D. | 2和14 |
5.若关于x的一元二次方程(m-1)x2+5x+m2-5m+4=0有一个根为0,则m的值等于( )
| A. | 1 | B. | 4 | C. | 1或4 | D. | 0 |
12.关于x的一元二次方程(m-1)x2+3x+m2-1=0的一根为0,则m的值是( )
| A. | -1 | B. | -2 | C. | ±1 | D. | ±2 |
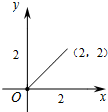
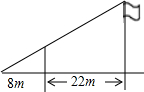 下列说法中正确的序号有②.
下列说法中正确的序号有②.