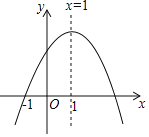Question

【题目】在平面直角坐标系xOy中，抛物线y＝ax2﹣2ax﹣3a与x轴交于A、B两点（点A在点B的左侧）．

（Ⅰ）求出点A、B的坐标；

（Ⅱ）当a＜0时，经过点A的直线l：y＝kx+a与y轴负半轴交于点C，与抛物线的另一个交点为D，点E是抛物线上的一个动点，且在直线l上方．

①若△ACE的面积的最大值为，求a的值；

②设P是抛物线的对称轴上的一点，点Q在抛物线上，当以点A、D、P、Q为顶点的四边形构成矩形时，请直接写出此时点P的坐标．

Answer 1

【答案】（Ⅰ）A（﹣1，0），B（3，0）；（Ⅱ）①﹣；②P1（1，﹣4），P2（1，﹣）．

【解析】

（Ⅰ）令y＝0，则ax2﹣2ax﹣3a＝0，可求点A、B的坐标；

（Ⅱ）①先求直线l的解析式，点E（m，am2﹣2am﹣3a），求出直线AE解析式，由三角形的面积公式可求△ACE的面积＝×（m﹣）2﹣a，即可求解；

②分以AD为边或对角线两种情况讨论即可．

解：（Ⅰ）令y＝0，则ax2﹣2ax﹣3a＝0，

解得x1＝﹣1，x2＝3

∵点A在点B的左侧，

∴A（﹣1，0），B（3，0）

（Ⅱ）①∵直线l：y＝kx+a经过点A，

∴0＝﹣k+a，

∴k＝a，

∴直线l：y＝ax+a，

如图1，过点E作EN⊥y轴，垂足为N，设AE与y轴的交点为M，

设点E（m，am2﹣2am﹣3a），yAE＝k1x+b，

则，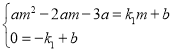

解得：，

∴yAE＝（am﹣3a）x+am﹣3a，M（0，am﹣3a）

∵MC＝am﹣3a﹣a＝am﹣4a，NE＝m

∴S△ACE＝S△ACM+S△CEM＝ [am﹣4a]×1+ [am﹣4a]m＝×（m﹣）2﹣a，

∵a＜0，

∴最大值﹣a＝，

∴a＝﹣；

②令ax2﹣2ax﹣3a＝ax+a，即ax2﹣3ax﹣4a＝0，

解得x1＝﹣1，x2＝4，

∴D（4，5a），

∵y＝ax2﹣2ax﹣3a，

∴抛物线的对称轴为x＝1，

设P1（1，m），

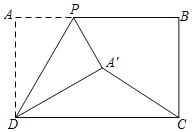
如图2，若AD是矩形的一条边，

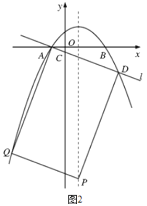
由AQ∥DP知xD﹣xP＝xA﹣xQ，可知Q点横坐标为﹣4，将x＝﹣4代入抛物线方程得Q（﹣4，21a），

m＝yD+yQ＝21a+5a＝26a，则P（1，26a），

∵四边形ADPQ为矩形，∴∠ADP＝90°，

∴AD2+PD2＝AP2，

∵AD2＝[4﹣（﹣1）]2+（5a）2＝52+（5a）2，

PD2＝（1﹣4）2+（26a﹣5a）2＝32+（21a）2，

∴[4﹣（﹣1）]2+（5a）2+（1﹣4）2+（26a﹣5a）2＝（﹣1﹣1）2+（26a）2，

即a2＝，

∵a＜0，

∴a＝﹣，

∴P1（1，﹣）．

如图3，若AD是矩形的一条对角线，

则线段AD的中点坐标为（，），Q（2，﹣3a），

m＝5a﹣（﹣3a）＝8a，则P（1，8a），

∵四边形AQDP为矩形，∴∠APD＝90°，

∴AP2+PD2＝AD2，

∵AP2＝[1﹣（﹣1）]2+（8a）2＝22+（8a）2，

PD2＝（4﹣1）2+（8a﹣5a）2＝32+（3a）2，

AD2＝[4﹣（﹣1）]2+（5a）2＝52+（5a）2，

∴22+（8a）2+32+（3a）2＝52+（5a）2，

解得a2＝，

∵a＜0，

∴a＝﹣，

∴P2（1，﹣4）．

综上可得，P点的坐标为P1（1，﹣4），P2（1，﹣）．