题目内容
二次函数y=ax2+bx+c图象上部分点的对应值如下表:
则当y≤0时,x的取值范围为 .
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
考点:二次函数的性质
专题:
分析:由表中数据可知抛物线y=ax2+bx+c与x轴的交点为(-2,0)、(3,0),然后根据表格确定y≤0的是x的取值范围.
解答:解:由表中数据可知抛物线y=ax2+bx+c与x轴的交点为(-2,0)、(3,0),
根据表格确定y≤0的是x的取值范围-2≤x≤3,
故答案为:-2≤x≤3.
根据表格确定y≤0的是x的取值范围-2≤x≤3,
故答案为:-2≤x≤3.
点评:考查了二次函数的性质,观察二次函数的对应值的表格,关键是寻找对称点,顶点坐标及对称轴,利用对称性解答.

练习册系列答案
相关题目
 如图,C、D是线段AB上两点,若CB=5cm,DB=9cm,且D是AC的中点,则AC的长等于( )
如图,C、D是线段AB上两点,若CB=5cm,DB=9cm,且D是AC的中点,则AC的长等于( )| A、6cm | B、9cm |
| C、8cm | D、13cm |
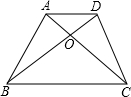 如图,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,∠ABC=75°,则△AOD与△BOC的面积之比( )
如图,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,∠ABC=75°,则△AOD与△BOC的面积之比( )| A、1:2 | ||
B、1:
| ||
| C、1:3 | ||
| D、1:4 |
 已知:如图所示,已知线段a、b、c(a>c).求作:线段AB,使AB=a+b-c.
已知:如图所示,已知线段a、b、c(a>c).求作:线段AB,使AB=a+b-c. 如图,过原点的直线分别交双曲线
如图,过原点的直线分别交双曲线