题目内容
1．解方程：（1）$\frac{x}{2x-5}$+$\frac{5}{5-2x}$=1；
（2）$\frac{1}{x+1}$+$\frac{2}{x-1}$=$\frac{4}{{x}^{2}-1}$．
分析 两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：（1）去分母得：x-5=2x-5，
解得：x=0，
经检验x=0是分式方程的解；
（2）去分母得：x-1+2x+2=4，
解得：x=1，
经检验x=1是增根，分式方程无解．
点评 此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
16．
如图，在四边形ABCD中，∠DAB=90°，∠DCB=90°，E、F分别是BD、AC的中点，AC=6，BD=10，则EF的长为（ ）
如图，在四边形ABCD中，∠DAB=90°，∠DCB=90°，E、F分别是BD、AC的中点，AC=6，BD=10，则EF的长为（ ）| A． | 3 | B． | 4 | C． | 5 | D． | $\sqrt{7}$ |
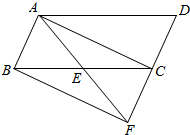如图，已知点E是?ABCD中BC边的中点，若∠ABE=∠BAE=60°，BC=4，连接AE并延长交DC的延长线于点F．
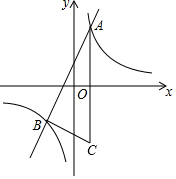已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A（1，4）和点B（-2，m），点C与点A关于x轴对称．