题目内容
8.已知△ABC中,AB=AC,BC=20,D是AB上一点,且CD=16,BD=12,(1)求证:CD⊥AB;
(2)求三角形ABC的周长.
分析 (1)由BC=20,CD=16,BD=12,计算得出BD2+DC2=BC2,根据勾股定理的逆定理即可证明CD⊥AB;
(2)设AD=x,则AC=x+12,在Rt△ACD中,利用勾股定理求出x,得出AC,继而可得出△ABC的周长.
解答 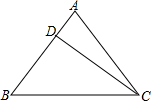 解:(1)在△BCD中,BC=20,CD=16,BD=12,
解:(1)在△BCD中,BC=20,CD=16,BD=12,
∵BD2+DC2=BC2,
∴△BCD是直角三角形,∠BDC=90°,
∴CD⊥AB;
(2)设AD=x,则AC=x+12,
在Rt△ADC中,∵AC2=AD2+DC2,
∴x2+162=(x+12)2,
解得:x=$\frac{14}{3}$.
∴△ABC的周长为:($\frac{14}{3}$+12)×2+20=$\frac{160}{3}$.
点评 本题考查了勾股定理及其逆定理的知识,解答本题的关键是利用勾股定理求出AD的长度,得出腰的长度,难度一般.

练习册系列答案
相关题目
17.下列命题中,真命题是( )
| A. | 若a>b,则a2>ab | B. | 若$\sqrt{(1-m)^{2}}$=m-1,则m≤1 | ||
| C. | 若a>b,则$\frac{1}{a}$<$\frac{1}{b}$ | D. | 已知a,b为实数,若a+b=1,则ab≤$\frac{1}{4}$ |
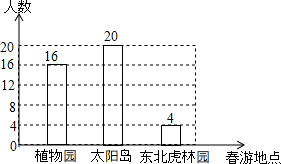 某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.
某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个).该校从八年级学生中随机抽取了a名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图. 如图,C,D为线段AB上两点,且AC=BD,AE∥BF.AE=BF.求证:∠E=∠F.
如图,C,D为线段AB上两点,且AC=BD,AE∥BF.AE=BF.求证:∠E=∠F.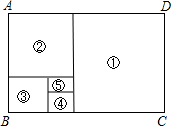 如图,在“黄金矩形”ABCD(即$\frac{宽AB}{长BC}$≈0.618)中,依次画正方形①、②、③、④
如图,在“黄金矩形”ABCD(即$\frac{宽AB}{长BC}$≈0.618)中,依次画正方形①、②、③、④ 如图,△ABC是直角三角形,∠ACB=90°.
如图,△ABC是直角三角形,∠ACB=90°.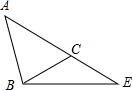 如图,在△ABE中,点C在AE上,AB=AC=5,∠CBE=$\frac{1}{2}$∠A,sin∠CBE=$\frac{\sqrt{5}}{5}$,求BC和BE的长.
如图,在△ABE中,点C在AE上,AB=AC=5,∠CBE=$\frac{1}{2}$∠A,sin∠CBE=$\frac{\sqrt{5}}{5}$,求BC和BE的长.