题目内容
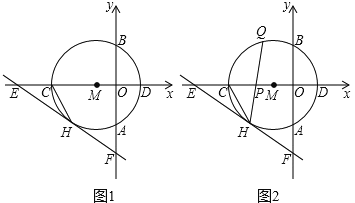
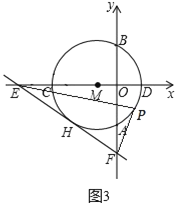
【题目】如图,点![]() 是
是![]() 上(除点
上(除点![]() 外)一点,以
外)一点,以![]() 为边作等边
为边作等边![]() ,与
,与![]() 交于两点.记
交于两点.记![]() 的长为
的长为![]() ,点
,点![]() 到
到![]() 的距离为
的距离为![]() ,点
,点![]() 到
到![]() 的距离为
的距离为![]() :
:
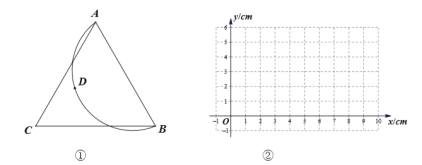
小腾根据学习函数的经验,对![]() ,
,![]() ,
,![]() 的长度之间的关系进行了探究.
的长度之间的关系进行了探究.
下面是小腾的探究过程,请补充完整:
(1)对于点![]() 在
在![]() 上的不同位置,画图、测量,得到了
上的不同位置,画图、测量,得到了![]() ,
,![]() ,
,![]() 的长度几组值,如下表:
的长度几组值,如下表:
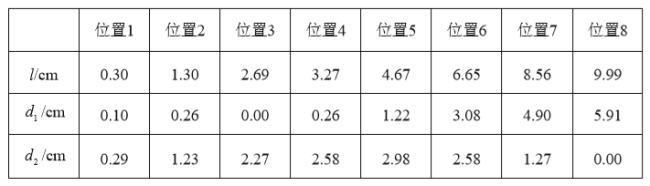
在![]() ,
,![]() ,
,![]() 的长度这三个量中,确定 是自变量, 和 都是这个自变量的函数;
的长度这三个量中,确定 是自变量, 和 都是这个自变量的函数;
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图像;
中,画出(1)中所确定的函数的图像;
(3)结合函数图像,解决问题:当点![]() 在
在![]() 平分线上时,
平分线上时,![]() 的长约为 cm.
的长约为 cm.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]()
【解析】
(1)根据题意,点![]() 是
是![]() 上(除点
上(除点![]() 外)的动点,分析即可得知
外)的动点,分析即可得知![]() 为自变量,
为自变量,![]() 、
、![]() 为这个自变量的函数;
为这个自变量的函数;
(2)在同一平面直角坐标系![]() 中,描点连线即可;
中,描点连线即可;
(3)根据角平分线性质,观察图像求解即可.
解:(1)根据题意,点![]() 是
是![]() 上(除点
上(除点![]() 外)的动点,且
外)的动点,且![]() 的长为
的长为![]() ,点
,点![]() 到
到![]() 的距离为
的距离为![]() ,点
,点![]() 到
到![]() 的距离为
的距离为![]() ,
,
∴![]() 为自变量,
为自变量,![]() 、
、![]() 为这个自变量的函数,
为这个自变量的函数,
故答案为:![]() ,
,![]() ,
,![]()
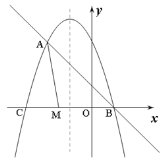
(2)在同一平面直角坐标系![]() 中描点,画图,所得函数图像如下:
中描点,画图,所得函数图像如下:

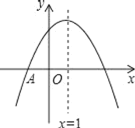
(3)∵点![]() 在
在![]() 平分线上,
平分线上,
∴![]() ,
,
∴两函数交点即为![]() 情况下的描点,
情况下的描点,
观察函数图像可知,此时![]() 约为6.4cm,
约为6.4cm,
∴当点![]() 在
在![]() 平分线上时,
平分线上时,![]() 的长约为6.4cm,
的长约为6.4cm,
故答案为:6.4.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目