题目内容
 完成推理填空:
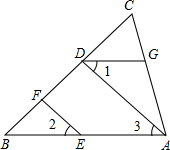
完成推理填空:如图,已知∠l=∠2,∠BAC=70°,∠AGD=110°.将证明EF∥AD的过程填写完整
证明:∵∠BAC=70°,∠ACD=110°
∴∠BAC+∠AGD=180°
∴
∴∠1=
又∵∠l=∠2.
∴∠2=∠3.
∴EF∥AD(
考点:平行线的判定与性质
专题:推理填空题
分析:求出∠BAC+∠AGD=180°,根据平行线的判定推出DG∥AB,推出∠1=∠3=∠2,根据平行线的判定推出即可.
解答:证明:∵∠BAC=70°,∠ACD=110°,
∴∠BAC+∠AGD=180°,
∴DG∥AB(同旁内角互补,两直线平行),
∴∠1=∠3(两直线平行,内错角相等),
∵∠1=∠2,
∴∠2=∠3,
∴EF∥AD(同位角相等,两直线平行),
故答案为:DG,AB,同旁内角互补,两直线平行,∠3,两直线平行,内错角相等,同位角相等,两直线平行.
∴∠BAC+∠AGD=180°,
∴DG∥AB(同旁内角互补,两直线平行),
∴∠1=∠3(两直线平行,内错角相等),
∵∠1=∠2,
∴∠2=∠3,
∴EF∥AD(同位角相等,两直线平行),
故答案为:DG,AB,同旁内角互补,两直线平行,∠3,两直线平行,内错角相等,同位角相等,两直线平行.
点评:本题考查了平行线的性质和判定的应用,注意:平行线的性质是:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
相关题目
 如图,下列说法中错误的是( )
如图,下列说法中错误的是( )| A、OA方向是北偏东15° |
| B、OB方向是西北方向 |
| C、OC方向是南偏西30° |
| D、OD方向是南偏东25° |
下列关系式中,表示y是x的正比例函数的是( )
A、y=
| ||
| B、y=1 | ||
| C、y=x+1 | ||
| D、y=2x |
有一段坡路,小明骑车上坡的速度为V1千米/小时,下坡的速度为V2千米/小时,那么小明在这段路上的平均速度为( )
A、
| ||
B、
| ||
C、
| ||
| D、无法确定 |
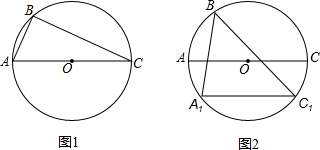 如图在⊙O中,图1中△ABC内接于⊙O且∠ABC=90°,图2中△A1BC1,内接于⊙O,AC是直径且AC∥A1C1,请仅用无刻度的直尺按要求画图.
如图在⊙O中,图1中△ABC内接于⊙O且∠ABC=90°,图2中△A1BC1,内接于⊙O,AC是直径且AC∥A1C1,请仅用无刻度的直尺按要求画图.