题目内容
 采用如下方法可以得到黄金分割点:如图,设AB是已知线段,经过点B作BD⊥AB,使BD=
采用如下方法可以得到黄金分割点:如图,设AB是已知线段,经过点B作BD⊥AB,使BD=| 1 |
| 2 |
考点:黄金分割
专题:常规题型
分析:设AB=2a,则BD=a,DE=a,根据勾股定理计算出AD=
a,则AE=AD-DE=(
-1)a,再利用画法得到AC=AE=(
-1)a,即AC=
AB,然后根据黄金分割的定义得到点C就是线段AB的黄金分割点.
| 5 |
| 5 |
| 5 |
| ||
| 2 |
解答:解:设AB=2a,则BD=a,DE=a,
在Rt△ABD中,AD=
=
a,
所以AE=AD-DE=
a-a=(
-1)a,
所以AC=AE=(
-1)a,
即AC=
AB,
所以点C就是线段AB的黄金分割点.
在Rt△ABD中,AD=
| AB2+BD2 |
| 5 |
所以AE=AD-DE=
| 5 |
| 5 |
所以AC=AE=(
| 5 |
即AC=
| ||
| 2 |
所以点C就是线段AB的黄金分割点.
点评:本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=
AB≈0.618AB,并且线段AB的黄金分割点有两个.
| ||
| 2 |

练习册系列答案
相关题目
 一次函数y=kx+b的图象如图所示,当y>0时,x的取值范围是( )
一次函数y=kx+b的图象如图所示,当y>0时,x的取值范围是( )| A、x>2 | B、x<2 |
| C、x>0 | D、x<0 |
 已知:如图,在四边形ABCD中,AB∥DC,BC=b,AB=AC=AD=a,求BD的长.
已知:如图,在四边形ABCD中,AB∥DC,BC=b,AB=AC=AD=a,求BD的长.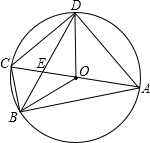 如图,四边形ABCD内接于⊙O,⊙O的直径AC=4,∠BCD=120°,BD与AC的交点为E.
如图,四边形ABCD内接于⊙O,⊙O的直径AC=4,∠BCD=120°,BD与AC的交点为E.