题目内容
在△ABC中∠A=50°，AB=AC=12cm，AB的垂直平分线分别交AC，AB于点D，E，△BCD的周长为19cm，求∠DBC的度数．
考点：线段垂直平分线的性质,等腰三角形的性质
专题：
分析：已知∠A=40°，AB=AC可得∠ABC=∠ACB，再由线段垂直平分线的性质可求出∠ABC=∠A，易求∠DBC．
解答：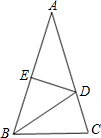
解：∵∠A=50°，AB=AC，
∴∠ABC=∠ACB=65°，
又∵DE垂直平分AB，
∴DB=AD
∴∠ABD=∠A=50°，
∴∠DBC=∠ABC-∠ABD=65°-50°=15°．
即∠DBC=15°．
解：∵∠A=50°，AB=AC，∴∠ABC=∠ACB=65°，
又∵DE垂直平分AB，
∴DB=AD
∴∠ABD=∠A=50°，
∴∠DBC=∠ABC-∠ABD=65°-50°=15°．
即∠DBC=15°．
点评：此题主要考查了等腰三角形的性质以及线段垂直平分线的性质．主要了解线段垂直平分线的性质即可求解．
练习册系列答案
相关题目
如图，小林种了一株高40cm的树苗，这株树苗平均每周长高5cm，几周后这株树苗的高超过1米？下列语句：
①两条直线相交所构成的四个角中有一个角是直角；
②两条直线相交所构成的四个角相等；
③两条直线相交所构成的对顶角互补；
④两条直线相交所构成的邻补角相等．
其中能判断两条直线垂直的有（ ）
①两条直线相交所构成的四个角中有一个角是直角；
②两条直线相交所构成的四个角相等；
③两条直线相交所构成的对顶角互补；
④两条直线相交所构成的邻补角相等．
其中能判断两条直线垂直的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
下列运算错误的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、（-
|