题目内容
13.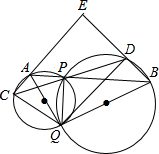 如图所示,两圆O1,O2相交于PQ两点,过P点有两条直线AB、CD,直线AB分别与两圆O1,O2交于点A、B(A、B在P点两侧),直线CD分别与两圆O1,O2交于点C、D(C、D在P点两侧),直线AC与BD交于点E.
如图所示,两圆O1,O2相交于PQ两点,过P点有两条直线AB、CD,直线AB分别与两圆O1,O2交于点A、B(A、B在P点两侧),直线CD分别与两圆O1,O2交于点C、D(C、D在P点两侧),直线AC与BD交于点E.(1)证明:∠AQC=∠BQD;
(2)若∠AQB=120°,求∠E.
分析 (1)利用圆周角定理得出:∠AQC=∠APC,∠BPD=∠DQB,进而求出答案;
(2)利用三角形的外角以及圆内接四边形的性质得出∠ACP+∠E+∠PQB=180°,进而得出答案.
解答 (1)证明:∵∠AQC=∠APC,∠BPD=∠DQB,
∠APC=∠BPD,
∴∠AQC=∠BQD;
(2)解:∵∠ACP=∠AQP,∠AQB=120°,
∴∠ACP+∠PQB=120°,
∵∠ACP+∠E=∠CDB,
∠CDB+∠PQB=180°,
∴∠ACP+∠E+∠PQB=180°,
∴∠AQP+∠E+∠PQB=180°,
则∠E+∠AQB=180°,
故∠E=180°-∠AQB=180°-120°=60°.
点评 此题主要考查了圆内接四边形的性质,圆周角定理以及三角形的外角等知识,熟练应用圆周角定理是解题关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.若a的倒数的相反数是8,b的相反数的倒数也是8,则( )
| A. | a=b | B. | a<b | C. | a>b | D. | ab=1 |
3.若把分式$\frac{2xy}{x+y}$中的x和y都扩大5倍,那么分式的值将( )
| A. | 扩大5倍 | B. | 扩大10倍 | C. | 不变 | D. | 缩小5倍 |
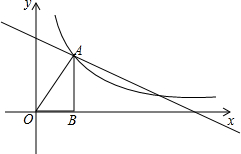 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A、C两点,点C坐标是(6,1),AB⊥x轴于点B,且AB=3.
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于A、C两点,点C坐标是(6,1),AB⊥x轴于点B,且AB=3.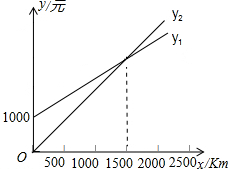 某单位计划与某个体车主或某国营出租车公司中的一家签订月租车合同,设汽车每月行驶x km,应付给个体车主的月租费为y1元,付给出租车公司的月租费为y2元,在同一直角坐标系中y1、y2与x的函数图象如图所示,观察图象回答下列问题:
某单位计划与某个体车主或某国营出租车公司中的一家签订月租车合同,设汽车每月行驶x km,应付给个体车主的月租费为y1元,付给出租车公司的月租费为y2元,在同一直角坐标系中y1、y2与x的函数图象如图所示,观察图象回答下列问题: