题目内容
 如图,已知PA,PB分别切⊙O于点A、B,⊙O的半径为6,∠P=60°,则阴影部分的面积为
如图,已知PA,PB分别切⊙O于点A、B,⊙O的半径为6,∠P=60°,则阴影部分的面积为考点:切线的性质,扇形面积的计算
专题:计算题
分析:连接OA、OB,连接OP,如图,根据切线的性质得OA⊥PA,OB⊥PB,根据切线长定理得PA=PB,∠OPA=∠OPB=
∠APB=30°,再利用四边形内角和得到∠AOB=180°-∠P=120°,接着在Rt△PAO中,根据含30度的直角三角形三边的关系计算出PA=
OA=6
,利用三角形模糊公式可计算出S四边形AOBP=2S△OAP=36
,然后利用扇形的面积公式和阴影部分的面积=S四边形AOBP-S扇形AOB进行计算.
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
解答:解:连接OA、OB,连接OP,如图,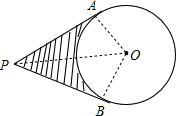
∵PA,PB分别切⊙O于点A、B,
∴OA⊥PA,OB⊥PB,PA=PB,∠OPA=∠OPB=
∠APB=30°,
∴∠OAP=∠OBP=90°,
而∠P=60°,
∴∠AOB=180°-∠P=120°,
在Rt△PAO中,∵OA=6,
∴PA=
OA=6
,
∴S四边形AOBP=2S△OAP=2•
•6•6
=36
,
∴阴影部分的面积=S四边形AOBP-S扇形AOB=36
-
=36
-12π.
故答案为36
-12π.

∵PA,PB分别切⊙O于点A、B,
∴OA⊥PA,OB⊥PB,PA=PB,∠OPA=∠OPB=
| 1 |
| 2 |
∴∠OAP=∠OBP=90°,
而∠P=60°,
∴∠AOB=180°-∠P=120°,
在Rt△PAO中,∵OA=6,
∴PA=
| 3 |
| 3 |
∴S四边形AOBP=2S△OAP=2•
| 1 |
| 2 |
| 3 |
| 3 |
∴阴影部分的面积=S四边形AOBP-S扇形AOB=36
| 3 |
| 120•π•62 |
| 360 |
| 3 |
故答案为36
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了切线长定理和扇形的面积公式.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
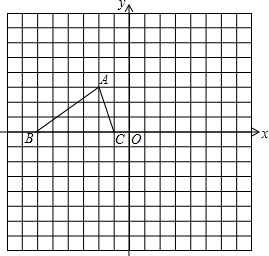 如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0). 已知二次函数y=x2-(m-2)x+m的图象过点(-1,15),
已知二次函数y=x2-(m-2)x+m的图象过点(-1,15),