题目内容
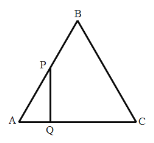
【题目】如图等边![]() 的边长为
的边长为![]() ,点
,点![]() ,点
,点![]() 同时从点
同时从点![]() 出发,点
出发,点![]() 沿
沿![]() 以
以![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 沿
沿![]() 以
以![]() 的速度也向点
的速度也向点![]() 运动,直到到达点
运动,直到到达点![]() 时两点都停止运动,若
时两点都停止运动,若![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,则下列最能反映
,则下列最能反映![]() 与
与![]() 之间函数关系的图象是( )
之间函数关系的图象是( )
A.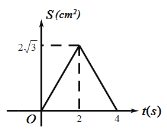 B.
B.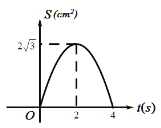
C.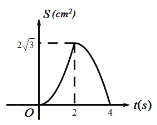 D.
D.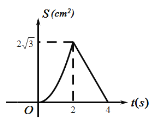
【答案】C
【解析】
先计算点P从点A运动到点B时![]() 的面积等式,再计算点P从点B运动到点C时
的面积等式,再计算点P从点B运动到点C时![]() 的面积等式,最后根据二次函数图象的性质即可得出答案.
的面积等式,最后根据二次函数图象的性质即可得出答案.
由等边三角形的性质得:![]()
由题意,分点P从点A运动到点B和点P从点B运动到点C两段
(1)点P从点A运动到点B
点P运动到点B时,时间为![]() ,此时点Q运动到AC的中点处
,此时点Q运动到AC的中点处
![]()
![]()
![]() 是直角三角形,
是直角三角形,![]()
则![]() 的面积为
的面积为![]()
(2)点P从点B运动到点C
点P运动到点C时,时间为![]() ,此时点Q运动到点C处
,此时点Q运动到点C处
如图,![]()
![]()
![]()
![]() 是直角三角形,
是直角三角形,![]()
则![]() 的面积为
的面积为![]()
综上,
根据二次函数图象的性质可得,只有C项符合题意
故选:C.


练习册系列答案
相关题目