题目内容
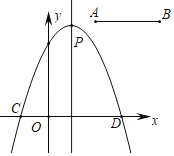
【题目】如图,抛物线![]() 的图像过点
的图像过点![]() ,顶点为
,顶点为![]()
![]() 求
求![]() 的值.
的值.
![]() 点
点![]() 以点
以点![]() 为旋转中心,顺时针旋转
为旋转中心,顺时针旋转![]() 得到点
得到点![]() ,判断点
,判断点![]() 是否落在抛物线上.
是否落在抛物线上.
![]() 第一象限内抛物线上有一点
第一象限内抛物线上有一点![]() 与
与![]() 相交于点
相交于点![]() ,当
,当![]() 时,求点
时,求点![]() 坐标.
坐标.

【答案】(1)![]() ;
;![]() =3(2)
=3(2)![]() 没有落在抛物线上;(3)
没有落在抛物线上;(3)![]()
【解析】
(1)由点![]() 、
、![]() 在抛物线
在抛物线![]() 的图像上,则满足函数关系式,代入计算即可求得答案;
的图像上,则满足函数关系式,代入计算即可求得答案;
(2)由(1)可得![]() ,再确定顶点
,再确定顶点![]() ,然后根据旋转的性质求得
,然后根据旋转的性质求得![]() ,最后将其代入函数关系式通过计算即可判断结论;
,最后将其代入函数关系式通过计算即可判断结论;
(3)通过添加辅助线根据相似三角形的判定和性质可得![]() ,由待定系数法求得直线
,由待定系数法求得直线![]() :
:![]() ,再将坐标代入解析式得到关于
,再将坐标代入解析式得到关于![]() 的方程,解方程确定
的方程,解方程确定![]() 的取值即可求得答案.
的取值即可求得答案.
解:(1)由抛物线与![]() 轴交于点
轴交于点![]() (0,3),
(0,3),
可得 ![]() =3,把
=3,把![]() (-1,0)代入
(-1,0)代入![]()
得![]() ,解得
,解得 ![]()
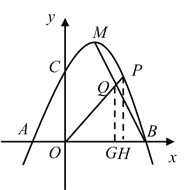
(2)如图:
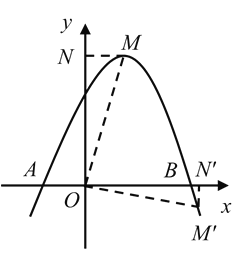
由(1)可得![]()
∴顶点为![]()
![]() ,
,![]()
∴![]() ,把
,把![]() 代入
代入![]()
![]()
![]()
![]()
∴![]() 没有落在抛物线
没有落在抛物线![]() 上
上
(3)过点![]() 、
、![]() 分别作
分别作![]() 、
、![]() ,如图:
,如图:
∵![]() 、
、![]()
∴![]()
∴![]()
∴![]()
∴设点![]()
∵![]() ,
,
∴![]()
∴![]()
∵直线![]() 过点
过点![]() ,
,![]()
∴直线![]() :
:![]()
∵点![]() 在直线
在直线![]() 上
上
∴将![]() 代入
代入![]()
解得:![]() 2
2
∴所求点![]() 的坐标为
的坐标为![]() .
.
故答案是:(1)![]() ;
;![]() =3(2)
=3(2)![]() 没有落在抛物线上;(3)
没有落在抛物线上;(3)![]()

练习册系列答案
相关题目