题目内容
5.一次函数y=kx+b(k≠0)满足条件:当x=2时,y=-3;当x=-1时,y=4.(1)求这个一次函数的解析式;
(2)求这个函数的图象与坐标轴围成的三角形的面积S.
分析 (1)设一次函数解析式为y=kx+b,再利用待定系数法把(2,5)和(-1,-1)代入函数解析式,可得关于k、b的方程组,再解方程组可得k、b的值,进而得到答案;
(2)根据函数解析式计算出当x=0时y的值,当y=0时,x的值,进而得到与两坐标轴的交点坐标,然后求三角形的面积即可.
解答 解:(1)设y=kx+b(k≠0).
∵当x=2时,y=-3;当x=-1时,y=4,
∴$\left\{\begin{array}{l}{2k+b=-3}\\{-k+b=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{7}{3}}\\{b=\frac{5}{3}}\end{array}\right.$,
∴一次函数解析式为y=-$\frac{7}{3}$x+$\frac{5}{3}$;
(2)当x=0时,y=$\frac{5}{3}$,
当y=0时,-$\frac{7}{3}$x+$\frac{5}{3}$=0,
解得x=$\frac{5}{7}$,
∴与坐标轴的交点坐标为(0,$\frac{5}{3}$)、($\frac{5}{7}$,0),
此函数与坐标轴围成的三角形面积:S=$\frac{1}{2}$×$\frac{5}{3}$×$\frac{5}{7}$=$\frac{25}{42}$.
点评 此题主要考查了待定系数法求一次函数解析式,以及一次函数与两坐标轴的交点坐标,关键是正确求出解析式.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
13.计算-2m2n+m2n的结果为( )
| A. | -1 | B. | 2 | C. | -m2n | D. | -3m4n2 |
20.下列运算正确的是( )
| A. | a5+a5=a10 | B. | a6÷a2=a4 | C. | (mn)-3=mn-3 | D. | -3(a-b)=-3a-3b |
10.化简分式$\frac{{a}^{2}}{a-b}$+$\frac{{b}^{2}}{b-a}$的结果是( )
| A. | a+b | B. | a-b | C. | $\frac{a+b}{a-b}$ | D. | $\frac{a-b}{a+b}$ |
15.某公司10名职工5月份工资统计如下表:
该公司10名职工5月份工资的众数和中位数分别是( )
| 工资/(元) | 4000 | 4200 | 4400 | 4600 |
| 人数 | 1 | 3 | 4 | 2 |
| A. | 4400,4400 | B. | 4400,4300 | C. | 4200,4200 | D. | 4200,4300 |
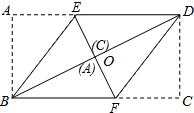 如图,将矩形纸片ABCD沿BE、DF折叠后,顶点A、C恰好都落在对角线BD的中点O处.若BD=6cm,则四边形BEDF的周长是8$\sqrt{3}$cm.
如图,将矩形纸片ABCD沿BE、DF折叠后,顶点A、C恰好都落在对角线BD的中点O处.若BD=6cm,则四边形BEDF的周长是8$\sqrt{3}$cm.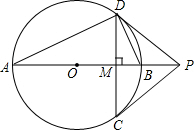 已知:如图,⊙O的直径AB垂直于弦CD于点M,过点C的切线与直径AB的延长线相交于点P,连结PD.
已知:如图,⊙O的直径AB垂直于弦CD于点M,过点C的切线与直径AB的延长线相交于点P,连结PD.