题目内容
如图，在△BCD中，∠BDC=90°，以BD为斜边，向外作Rt△ABD．若AD=4，∠ADB=∠C．且P是BC边上一动点，则DP长的最小值为4
4
．分析：根据等角的余角相等求出∠ABD=∠CBD，再根据垂线段最短可得DP⊥BC时DP的长度最小，然后根据角平分线上的点到角的两边的距离相等可得DP=AD．
解答：
解：∵∠BDC=90°，∠A=90°，
∴∠ABD+∠ADB=90°，
∠C+∠CBD=90°，
∵∠ADB=∠C，
∴∠ABD=∠CBD，
由垂线段最短可知DP⊥BC时DP的长度最小，
此时，DP=AD，
∵AD=4，
∴DP的最小值为4．
故答案为：4．
解：∵∠BDC=90°，∠A=90°，∴∠ABD+∠ADB=90°，
∠C+∠CBD=90°，
∵∠ADB=∠C，
∴∠ABD=∠CBD，
由垂线段最短可知DP⊥BC时DP的长度最小，
此时，DP=AD，
∵AD=4，
∴DP的最小值为4．
故答案为：4．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，由垂线段最短判断出点P的位置是解题的关键．
练习册系列答案
相关题目
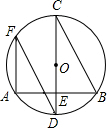（2013•朝阳区二模）如图，在⊙O中，直径CD⊥弦AB于点E，点F在弧AC上，若∠BCD=32°，则∠AFD的度数为
如图，在△BCD中，BE平分∠DBC交CD于F，延长BC至G，CE平分∠DCG，且EC、DB的延长线交于A点，若∠A=33°，∠DFE=63°．
如图，在△BCD中，BE平分∠DBC交CD于F，延长BC至G，CE平分∠DCG，且EC、DB的延长线交于A点，若∠A=33°，∠DFE=63°．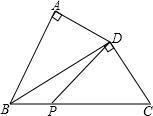
如图，在△BCD中，∠BDC=90°，以BD为斜边，向外作Rt△ABD．若AD=4，∠ADB=∠C．且P是BC边上一动点，则DP长的最小值为________．