题目内容
如图所示的梯形，AB=2
，α=30°，BC=8，∠D=60°，求：梯形ABCD的面积．
解：作AE⊥BC、BF⊥BC，
∵BC=8，α=30°，
∴CF=8×cos30°=4，BF=8×sin30°=4，
∵tanD=
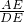，∴DE=
=
，
∴CD=DE+EF+FC=
，
∴梯形ABCD的面积为
（CD+AB）BF=×（+2）×4=
．
分析：根据α和BC即可求得BF、CF的值，根据AE即可求得DE的值，即可求得CD的值，进而可以计算梯形ABCD的面积．
点评：本题考查了特殊角的三角函数值，考查了三角函数值在直角三角形中的运用，考查了梯形面积的计算．
∵BC=8，α=30°，
∴CF=8×cos30°=4
，BF=8×sin30°=4，∵tanD=
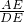，∴DE==，∴CD=DE+EF+FC=
，∴梯形ABCD的面积为
（CD+AB）BF=×（+2）×4=．分析：根据α和BC即可求得BF、CF的值，根据AE即可求得DE的值，即可求得CD的值，进而可以计算梯形ABCD的面积．
点评：本题考查了特殊角的三角函数值，考查了三角函数值在直角三角形中的运用，考查了梯形面积的计算．
练习册系列答案
相关题目
在数学活动课上小明给小亮出了一道题．要求做一梯形纸板，其中一底边长为10cm，高为12cm，两腰长分别为15cm和20cm．小亮按要求做出来如图所示的梯形纸板ABCD，其中AD∥BC，AD=10cm，AB=15cm，CD=20cm，小明说小亮只画出了其中一种图形．请你帮小亮画出其他图形，并求出每种图形中对应的另一底边的长．
，α=30°，BC=8，∠D=60°，求：梯形ABCD的面积．