题目内容
8、已知|n|≤20,n是整数且能使x2+x+n能在有理数范围内分解为两个一次式的乘积.则满足条件的n的个数是
5
个.分析:设x2+x+n分解为(x-a)(x+a+1),其中a为整数,所以(x-a)(x+a+1)=a2+x-a2-a,得到n=-a2-a,解不等式|a2+a|<20,求出a的值,然后把a的值代入n=-a2-a中确定n的值.
解答:解:因为n是整数且能使x2+x+n能在有理数范围内分解为两个一次式的乘,
所以设x2+x+n=(x-a)(x+a+1),a为整数,
得到n=-a2-a,
∵|n|≤20,∴|-a2-a|≤20
解得,-5≤a≤4的整数,
分别把a=-5,-4,-3,-2,-1,0,1,2,3,4代入n=-a2-a得到n=20,12,6,2,0.
所以满足条件的n的个数是5个.
故答案是:5.
所以设x2+x+n=(x-a)(x+a+1),a为整数,
得到n=-a2-a,
∵|n|≤20,∴|-a2-a|≤20
解得,-5≤a≤4的整数,
分别把a=-5,-4,-3,-2,-1,0,1,2,3,4代入n=-a2-a得到n=20,12,6,2,0.
所以满足条件的n的个数是5个.
故答案是:5.
点评:本题考查的是一元二次方程的整数根与有理数,根据二次三项式分解为两个一次式的乘积,得到两个一次式的所有情况,然后确定n的值.

练习册系列答案
相关题目
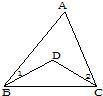 17、如图,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC(小于平角)的度数为
17、如图,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC(小于平角)的度数为 10、如图,直线AB、PQ与圆相切,切点分别为A、Q,已知a=20°,b=30°,c=40°,下面哪一个是x的值( )
10、如图,直线AB、PQ与圆相切,切点分别为A、Q,已知a=20°,b=30°,c=40°,下面哪一个是x的值( )