题目内容
【题目】如图，在边长为1的正方形网格中，有一格点△ABC，已知A、B、C三点的坐标分别是A（1，0）、B（2，－1）、C（3，1）．
(1) 请在网格图形中画出平面直角坐标系；
(2) 以原点O为位似中心，将△ABC放大2倍，画出放大后的△A′B′C′；
(3) 写出△A′B′C′各顶点的坐标，
(4) 写出△A′B′C′的重心坐标.
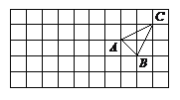
【答案】（1）如图所示见解析；（2）如图所示见解析；（3）A（﹣2，0），B（﹣4，2），C（﹣6，﹣2）；（4）重心坐标（﹣4，0）.
【解析】
（1）根据所给的已知点的坐标画直角坐标系；
（2）连接
、
、
，并延长到
、
、
长度找到各点的对应点，顺次连接即可；
（3）从坐标系中读出各点的坐标即可；
（4）要写出重心的坐标，先要作出重心，即三条中线的交点，再从坐标系中读出它的坐标.
（1）如图所示；（2）如图所示；
（3）从图可知：A（﹣2，0），B（﹣4，2），C（﹣6，﹣2）；
（4）
从图上可知重心坐标（﹣4，0）.
练习册系列答案
中考解读考点精练系列答案
相关题目
