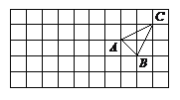题目内容
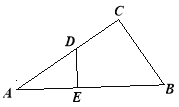
【题目】如图,在△ABC中,∠ACB=![]() ,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求![]() 的值;
的值;
(2)当![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据条件证明∠ADE=∠B,然后在Rt△ABC中,求cosB的值即可;(2)设AD为x,表示出DE=DC=![]() ,然后根据
,然后根据![]() ,列方程解答即可;也可证明△
,列方程解答即可;也可证明△![]() ∽△
∽△![]() ,利用相似三角形的对应必成比例得出
,利用相似三角形的对应必成比例得出![]() ,然后可求出AD的长.
,然后可求出AD的长.
试题解析:解法一:如图,(1)∵DE⊥AB,
∴∠DEA=90°.
∴∠A+∠ADE=90°.
∵∠ACB=![]() ,
,
∴∠A+∠B=90°.
∴∠ADE=∠B.
在Rt△ABC中,∵AC=12,BC=5,
∴AB=13.
∴![]() .
.
∴![]() .
.
(2)由(1)得![]() ,
,
设![]() 为
为![]() ,则
,则![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
解得![]() .
.
∴ ![]() .
.
解法二:(1)∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴△![]() ∽△
∽△![]() .
.
∴![]() .
.
在Rt△![]() 中,∵
中,∵![]() ,
,
∴![]()
∴![]()
∴![]()
(2)由(1)可知 △![]() ∽△
∽△![]() .
.
∴ ![]()
设![]() ,则
,则![]() .
.
∴![]() .
.
解得![]() .
.
∴![]() .
.

练习册系列答案
相关题目