题目内容
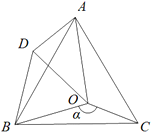
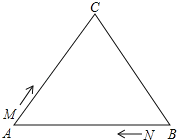
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在线段
在线段![]() 上,现将
上,现将![]() 沿着
沿着![]() 翻折后得到
翻折后得到![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 且
且![]() ,若
,若![]() ,则
,则![]() 的面积为__________.
的面积为__________.
【答案】![]()
【解析】
根据翻折的性质得到![]() ,由
,由![]() 且
且![]() ,依据平行线的性质及ASA,可得
,依据平行线的性质及ASA,可得![]() ≌
≌![]() ,通过等量代换得到
,通过等量代换得到![]() ,从而得到
,从而得到![]() 设为
设为![]() ,依据等量代换得到
,依据等量代换得到![]() ,依据三角形外角的性质、翻折的性质、三角形内角和定理得到
,依据三角形外角的性质、翻折的性质、三角形内角和定理得到![]() ,连接
,连接![]() 与
与![]() 的中点
的中点![]() ,依据三线合一求出两个有公共直角边的直角三角形,依据勾股定理列出关于
,依据三线合一求出两个有公共直角边的直角三角形,依据勾股定理列出关于![]() 的方程,解出可求得
的方程,解出可求得![]() 的底和高,再运用三角形面积公式即可.
的底和高,再运用三角形面积公式即可.
解:设![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵将![]() 沿着
沿着![]() 翻折后得到
翻折后得到![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ≌
≌![]() (ASA),
(ASA),
∴![]() ,
,![]() ,
,
又∵![]() ,
,![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,![]()
∴![]() ,
,
∴![]() ,
,
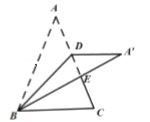
如下图,连接![]() 与
与![]() 的中点
的中点![]() ,则
,则![]() ,
,![]() ,
,

∴![]() ,
,
∴![]() ,即
,即![]() (
(![]() ),
),
解得![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目