题目内容
 如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=3cm,⊙O的半径为
如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=3cm,⊙O的半径为| 3 |
| A、45° | B、30° |
| C、90° | D、60° |
考点:垂径定理,特殊角的三角函数值
专题:
分析:先根据垂径定理得出CE=
CD,在Rt△OCE中,根据锐角三角函数的定义以及特殊角的三角函数值即可求出∠COB的度数,再由圆周角定理求出∠CDB的度数即可.
| 1 |
| 2 |
解答:解:∵AB是⊙O的直径,弦CD⊥AB于点E,
∴CE=
CD=
×3=
cm,
在Rt△OCE中,
∵sin∠COB=
=
=
∴∠COB=60°,
∴∠CDB=
∠BOC=
×60°=30°,
故选:B.
∴CE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
在Rt△OCE中,
∵sin∠COB=
| CE |
| OC |
| ||
|
| ||
| 2 |
∴∠COB=60°,
∴∠CDB=
| 1 |
| 2 |
| 1 |
| 2 |
故选:B.
点评:本题考查的是垂径定理、圆周角定理及特殊角的三角函数值等知识,熟知垂径定理是解答此题的关键.

练习册系列答案
相关题目
下列各组数据能构成直角三角形的是( )
| A、2,3,5 |
| B、5,8,10 |
| C、8,15,17 |
| D、10,12,16 |
下列说法中,正确的是( )
| A、一组数据8,8,7,10,6,8,9的众数和中位数都是8 | ||
| B、为了了解一批炮弹的杀伤半径,应采用普查的调查方式 | ||
C、一个游戏中奖的概率是
| ||
| D、若甲组数据的方差是0.1,乙组数据的方差是0.2,则乙组数据比甲组数据波动小 |
下面四个图形中,∠1与∠2相等的图形有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
在等边三角形、矩形、菱形、正方形、正五边形、正六边形中是中心对称的图形有( )个.
| A、3 | B、4 | C、5 | D、6 |
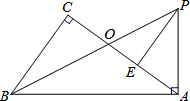 如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.
如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.