题目内容
如图1,AB是⊙O的直径,点C在AB的延长线上,AB=4,BC=2,P是⊙O上半部分的一个动点,连接OP,CP.
(1)求△OPC的最大面积;
(2)求∠OCP的最大度数;
(3)如图2,延长PO交⊙O于点D,连接DB,当CP=DB时,求证:CP是⊙O的切线.
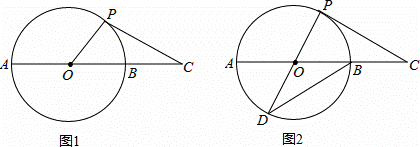
(1)解:∵AB=4,
∴OB=2,OC=OB+BC=4.
在△OPC中,设OC边上的高为h,
∵S△OPC=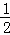 OC•h=2h,
OC•h=2h,
∴当h最大时,S△OPC取得最大值.
观察图形,当OP⊥OC时,h最大,如答图1所示:
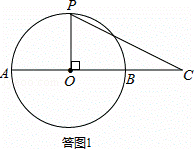
此时h=半径=2,S△OPC=2×2=4.
∴△OPC的最大面积为4.
(2)解:当PC与⊙O相切时,∠O CP最大.如答图2所示:
CP最大.如答图2所示:
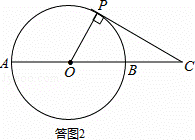
∵tan∠OCP=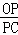 =
=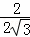 =
=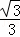 ,
,
∴∠OCP=30°
∴∠OCP的最大度数为30°.
(3)证明:如答图3,连接AP,BP.
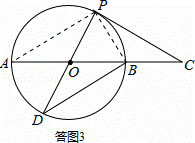
∴∠A=∠D=∠APD=∠ABD,
∵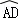 =
=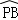 ,
,
∴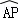 =
=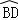 ,
,
∴AP=BD,
∵CP=DB,
∴AP=CP,
∴∠A=∠C
∴∠A=∠D=∠APD=∠ABD∠C,
在△ODB与△BPC中
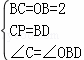 ,
,
∴△ODB≌△BPC(SAS),
∴∠D=∠BPC,
∵PD是直径,
∴∠DBP=90°,
∴∠D+∠BPD=90°,
∴∠BPC+∠BPD=90°,
∴DP⊥PC,
∵DP经过圆心,
∴PC是⊙O的切线.

下列计算正确的是( )
|
| A. | 2a+5a=7a | B. | 2x﹣x=1 | C. | 3+a=3a | D. | x2•x3=x6 |
如图1,将一个边长为a的 正方形纸片剪去两个小矩形,得到一个“
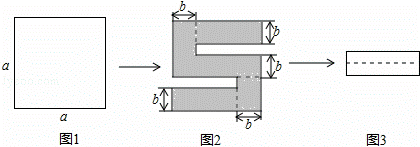
正方形纸片剪去两个小矩形,得到一个“ ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
|
| A. | 2a﹣3b | B. | 4a﹣8b | C. | 2a﹣4b | D. | 4a﹣10b |
已知a>b且a+b=0,则( )
|
| A. | a<0 | B. | b>0 | C. | b≤0 | D. | a>0 |
对坐标平面内不同两点A(x1,y1)、B(x2,y2),用|AB|表示A、B两点间的距离(即线段AB的长度),用‖AB‖表示A、B两点间的格距,定义A、B两点间的格距为‖AB‖=|x1﹣x2|+|y1﹣y2|,则|AB|与‖AB‖的大小关系为( )
|
| A. | |AB|≥‖AB‖ | B. | |AB|>‖AB‖ | C. | |AB|≤‖AB‖ | D. | |AB|<‖AB‖ |
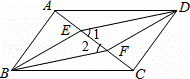
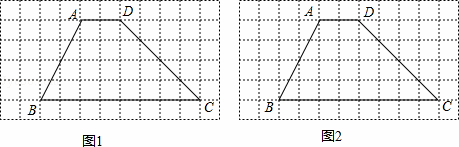

 的图象在其每个象限内,y随x的增大而增大,则k的值可以是 (答案不唯一) .(写出一个k的值)
的图象在其每个象限内,y随x的增大而增大,则k的值可以是 (答案不唯一) .(写出一个k的值)