Question

如图，ABCD为正五边形，点P为CD中点，连接BD，分别与AC、AP相交于点M、N，则=________．

Answer 1

分析：利用正五边形的内角度数以及相似三角形的性质即可得出，MN，BM的长度，即可得出比值．
解答：解：∵ABCD为正五边形，点P为CD中点，
∴∠BCA=∠BAC=36°，∠BAE=∠ABC=∠BCD=∠CDE=∠E=108°，
AP是CD的垂直平分线，
∴CN=ND，
∴∠NDC=∠NCD=36°，
∴∠BCN=∠BNC=72°，
∴∠CBN=36°，
∵∠NCM=108°-∠BCA-∠NCD=36°，
∠CNM=∠NCD+∠NDC=72°，
∴∠CMN=72°，
∴∠NCM=∠CBN，∠BCN=∠CNM，
∴△CNM∽△BCN，
=，
设BC=1，CN=BM=CM=x，则MN=1-x，
∴=，
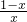∴x²+x-1=0，
解得：x=，
∴MN=1-=，
∴则==，
故答案为：．
点评：此题主要考查了正多边形的性质以及相似三角形的性质，利用正五边形性质得出△CNM∽△BCN进而求出MN，BM的长是解题关键．