题目内容
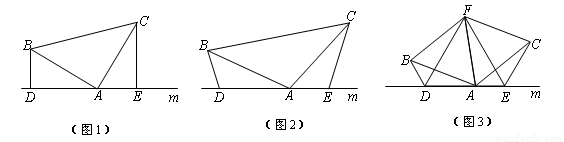
如图,  和
和 均为等边三角形,连接BE、CD.
均为等边三角形,连接BE、CD.

1.(1)请判断:线段BE与CD的大小关系是 ;
2.(2)观察图,当 和
和 分别绕点A旋转时,BE、CD之间的大小关系是否会改变?
分别绕点A旋转时,BE、CD之间的大小关系是否会改变?

3.(3)观察图3和4,若四边形ABCD、DEFG都是正方形,猜想类似的结论是 ,在图4中证明你的猜想.

4.(4)这些结论可否推广到任意正多边形(不必证明),如图5,BB1与EE1的关系是 ;它们分别在哪两个全等三角形中 ;请在图6中标出较小的正六边形AB1C1D1E1F1的另五个顶点,连接图中哪两个顶点,能构造出两个全等三角形?

【答案】
1.(1)线段BE与CD的大小关系是BE=CD……1分
2.(2)线段BE与CD的大小关系不会改变…2分
3.(3)AE=CG……………………………4分
证明: 如图,正方形ABCD与正方形DEFG中,
∵ AD=CD,DE=DG,∠ADC=∠GDE=90o…5分
又 ∠CDG=90o +∠ADG=∠ADE………6分
∴ △ADE≌△CDG.………………7分
∴AE=CG ………………8分
4.(4)这些结论可以推广到任意正多边形。如图9-5,BB1=EE1, 它们分别在△AE1E和△AB1B中.
 如图9-6,连接FF1,可证△AB1B≌△AF1F………………12分
如图9-6,连接FF1,可证△AB1B≌△AF1F………………12分
(若将字母顺时针标出,并回答正确也可得分)
【解析】略

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
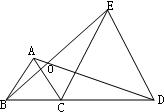
 15、如图,△ABC和△ADE均为等边三角形,B,D,E三点在同一条直线上,若∠ACE=20°,则∠BAD=
15、如图,△ABC和△ADE均为等边三角形,B,D,E三点在同一条直线上,若∠ACE=20°,则∠BAD=
 如图,△ABC和△ECD均为等边三角形,B、C、D三点共线,AD与BE相交于点O,则∠BOD=
如图,△ABC和△ECD均为等边三角形,B、C、D三点共线,AD与BE相交于点O,则∠BOD=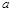 ,其中
,其中