题目内容
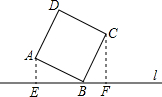 如图,直线l经过正方形ABCD的顶点B,点A、C到直线l的距离分别是1、2,则正方形的边长是
如图,直线l经过正方形ABCD的顶点B,点A、C到直线l的距离分别是1、2,则正方形的边长是考点:全等三角形的判定与性质,勾股定理,正方形的性质
专题:计算题
分析:由ABCD为正方形,利用正方形的性质得到∠ABC为直角,且AB=BC,利用平角的定义得到一对角互余,再由AE与CF都与直线l垂直,得到一对直角相等,在直角三角形ABE中,得到两个锐角互余,利用同角的余角相等得到一对角相等,利用AAS得到三角形ABE与三角形CBF全等,利用全等三角形的对应边相等得到AE=BF=1,EB=CF=2,利用勾股定理求出AB的长,即为正方形的边长.
解答:解:∵ABCD为正方形,
∴∠ABC=90°,AB=BC,
∴∠ABE+∠CBF=90°,
∵AE⊥l,CF⊥l,
∴∠AEB=∠BFC=90°,
∴∠ABE+∠BAE=90°,
∴∠BAE=∠CBF,
在△ABE和△CBF中,
,
∴△ABE≌△CBF(AAS),
∴AE=BF=1,EB=CF=2,
在Rt△ABE中,根据勾股定理得:AB=
=
,
则正方形的边长为
.
故答案为:
.
∴∠ABC=90°,AB=BC,
∴∠ABE+∠CBF=90°,
∵AE⊥l,CF⊥l,
∴∠AEB=∠BFC=90°,
∴∠ABE+∠BAE=90°,
∴∠BAE=∠CBF,
在△ABE和△CBF中,
|
∴△ABE≌△CBF(AAS),
∴AE=BF=1,EB=CF=2,
在Rt△ABE中,根据勾股定理得:AB=
| AE2+EB2 |
| 5 |
则正方形的边长为
| 5 |
故答案为:
| 5 |
点评:此题考查了全等三角形的判定与性质,勾股定理,以及正方形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
计算
的结果为( )
| 81 |
| A、±9 | B、±3 | C、9 | D、3 |
下列计算错误的是( )
| A、(x+1)(x2-x+1)=x3+1 |
| B、(x+2)2=x2+4x+4 |
| C、(x-1)(x+1)=x2+1 |
| D、(x-1)2=x2-2x+1 |
 已知有理数a、b在数轴上表示如图,比较a与-b大小为a
已知有理数a、b在数轴上表示如图,比较a与-b大小为a