题目内容
15.在Rt△ABC中,∠C=90,∠A=30°,AB=6,P是AB上的一点,过点P的直线折叠此三角形,使点A的对称点落在BC边上,则AP的取值范围是12$\sqrt{3}$≤PA≤3.分析 设点A的对应点为点A′,由翻折的性质可知:PA=PA′,由垂线段最短可知PA′⊥BC时,PA′最短即PA有最小值,当点A′与点B或点C重合时,PA有最大值.然后画出图形进行计算即可.
解答 解:设点A的对应点为点A′,由翻折的性质可知:PA=PA′.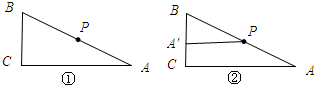
①如图①,当点A′与点B或点C重合时,PA有最大值.PA=$\frac{1}{2}AB=\frac{1}{2}×6=3$;
②如图②,当PA′⊥BC时,PA有最小值.
在Rt△ACB中,∠A=30°,
∴$\frac{AC}{AB}=\frac{\sqrt{3}}{2}$,即$\frac{AC}{6}=\frac{\sqrt{3}}{2}$.
∴AC=3$\sqrt{3}$.
∵A′P⊥BC,AC⊥BC,
∴A′P∥AC.
∴△A′BP∽△CBA.
∴$\frac{A′P}{CA}=\frac{PB}{AB}$.
设:PA=PA′=x,则PB=6-x,
∴$\frac{x}{3\sqrt{3}}=\frac{6-x}{6}$.
解得:x=12$\sqrt{3}$-18.
∴12$\sqrt{3}$≤PA≤3.
故答案为:12$\sqrt{3}$≤PA≤3.
点评 本题主要考查的是翻折的性质、特殊锐角三角函数值以及相似三角形的性质的应用,根据题意画出图形是解题的关键.

练习册系列答案
相关题目
7.将一张面值50元的人民币,兑换成5元或10元的零钱,那么兑换方案共有( )
| A. | 5种 | B. | 6种 | C. | 7种 | D. | 8种 |
5.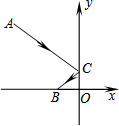 如图,一束光线从点A(-3,3)出发,经过y轴上的点C反射后经过点B(-1,0),则光线从点A到点B经过的路线长是( )
如图,一束光线从点A(-3,3)出发,经过y轴上的点C反射后经过点B(-1,0),则光线从点A到点B经过的路线长是( )
 如图,一束光线从点A(-3,3)出发,经过y轴上的点C反射后经过点B(-1,0),则光线从点A到点B经过的路线长是( )
如图,一束光线从点A(-3,3)出发,经过y轴上的点C反射后经过点B(-1,0),则光线从点A到点B经过的路线长是( )| A. | 3 | B. | $\frac{7}{2}$ | C. | 5 | D. | 6 |
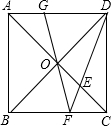 如图,O为正方形ABCD对角线的交点,E是线段OC的中点,DE的延长线交BC边于点F,连接并延长FO交AD于点G.若AB=2,则GF=$\frac{2\sqrt{10}}{3}$.
如图,O为正方形ABCD对角线的交点,E是线段OC的中点,DE的延长线交BC边于点F,连接并延长FO交AD于点G.若AB=2,则GF=$\frac{2\sqrt{10}}{3}$.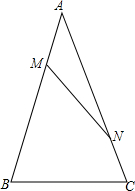 如图,已知△ABC中,AB=AC,AM=CN,探求:∠ABC与∠ANM满足∠B-∠ANM=30°时,$\frac{MN}{BC}$=$\frac{\sqrt{3}}{3}$.
如图,已知△ABC中,AB=AC,AM=CN,探求:∠ABC与∠ANM满足∠B-∠ANM=30°时,$\frac{MN}{BC}$=$\frac{\sqrt{3}}{3}$.