题目内容
【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 两点,其中点
两点,其中点![]() 的横坐标是
的横坐标是![]() .
.
⑴求这条直线的函数关系式及点![]() 的坐标 ;
的坐标 ;
⑵在![]() 轴上是否存在点
轴上是否存在点![]() ,使得△
,使得△![]() 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
⑶过线段![]() 上一点
上一点![]() ,作
,作![]() ∥
∥![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 在第一象限;点
在第一象限;点![]() ,当点
,当点![]() 的横坐标为何值时,
的横坐标为何值时, ![]() 的长度最大?最大值是多少?
的长度最大?最大值是多少?

【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 的横坐标为6时,
的横坐标为6时, ![]() 的长度最大值为18.
的长度最大值为18.
【解析】⑴关键是求直线的解析式,由于直线上有一点为![]() ,所以再找一个点即可求出直线的解析式;
,所以再找一个点即可求出直线的解析式; ![]() 的横坐标是
的横坐标是![]() 代入抛物线的解析式即可求出它的纵坐标,利用待定系数法可求直线的函数关系式;由于点
代入抛物线的解析式即可求出它的纵坐标,利用待定系数法可求直线的函数关系式;由于点![]() 是两个函数图象的交点,所以把两个函数联立起来,利用方程思想可以解决问题.
是两个函数图象的交点,所以把两个函数联立起来,利用方程思想可以解决问题.
⑵先假设存在,在假设存在的情况下还要分类讨论,因为没有指明直角顶点,所以要分成三种情况来讨论,利用勾股定理建立方程可以解决问题.
⑶利用![]() 的横坐标分别表示出线段
的横坐标分别表示出线段![]() 的长度,再利用
的长度,再利用![]() 建立函数关系,再根据函数关系来求最值.
建立函数关系,再根据函数关系来求最值.
解:⑴∵直线与抛物线交点![]() 的横坐标是
的横坐标是![]() ,
,
∴![]() ,
,
∴点![]() 的坐标是
的坐标是![]()
设此直线的解析式为![]() ,
,
将![]() 代入得
代入得![]() ,
,
解得: 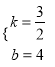 ,
,
∴此直线的解析式为![]() .
.
∵直线和抛物线交于![]() 两点,
两点,
∴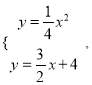
解得: ![]() 或
或![]()
∴点![]() 的坐标为
的坐标为![]() .
.
⑵.如备用图,点![]() 在
在![]() 轴上,连接
轴上,连接![]() .
.
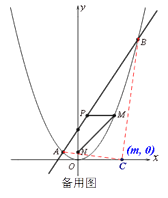
∵![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
若设存在的点![]() 的坐标为
的坐标为![]() ,则:
,则:
![]() ,
,
![]() ,
,
①.当![]() 时,
时, ![]() ,即
,即![]() ,
,
解得: ![]() .
.
②.当![]() 时,
时, ![]() ,即
,即![]()
解得: ![]() 或
或![]() .
.
③.当![]() 时,
时, ![]() ,即
,即![]()
解得: ![]() .
.
∴求出点![]() 的坐标为
的坐标为![]() .
.
⑶.设点![]() ,设
,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ;
;
在![]() △
△![]() 中,由勾股定理的:
中,由勾股定理的: 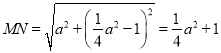 ,
,
又∵点![]() 与点
与点![]() 的纵坐标相同,∴
的纵坐标相同,∴![]() ,
,
∴![]() ,即点
,即点![]() 的横坐标为
的横坐标为![]() ,
,
∴![]() ,
,
∴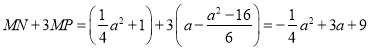 ,
,
∴当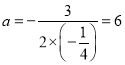 时,又∵
时,又∵![]() ,取值最大值取到18.
,取值最大值取到18.
∴当![]() 的横坐标为6时,
的横坐标为6时, ![]() 的长度最大值为18.
的长度最大值为18.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目



