Question

【题目】已知抛物线的图象与轴有两个公共点．

（1）求的取值范围，写出当取其范围内最大整数时抛物线的解析式；

（2）将（1）中所求得的抛物线记为，

①求的顶点的坐标；

②若当时， 的取值范围是，求的值；

（3）将平移得到抛物线,使的顶点落在以原点为圆心半径为的圆上，求点与两点间的距离最大时的解析式，怎样平移可以得到所求抛物线？

Answer 1

【答案】（1）;(2) ①,②1；（3）的解析式为．将抛物线记为向左平移,再向上平移即可得到抛物线．

【解析】试题分析：（1）函数图形与x轴有两个公共点，则该函数为二次函数且△＞0，故此可得到关于m的不等式组，从而可求得m的取值范围；

（2）①把（1）中求得的函数解析式改为顶点式，即可得出顶点P的坐标；

②先求得抛物线的对称轴，当1≤x≤n时，函数图象位于对称轴的右侧，y随x的增大而增大，当x＝n时，y有最大值2n，然后将x＝n，y＝2n代入求解即可；

（3）由弦的性质可得当PQ经过圆心时，PQ有最大值，此时Q点位于第二象限．根据点P、O的坐标，求得直线OP的解析式，设出点Q的坐标，根据点Q在直线PO上，以及点Q到原点的距离是即可求出点Q的坐标，进而得出C2的解析式，得出C2如何由C1平移得到．

试题解析：

解：（1）由题意可得： ，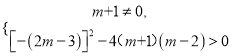

解得： 且

当取最大整数时，其值为2，此时函数解析式为： ．

（2）①由，顶点的坐标为.

②抛物线C1的对称轴为，

∴当时， 随的增大而增大．

∵当时， 的取值范围是，

∴，

∴或（舍去）．

∴．

（3）由弦的性质，当线段经过圆心时， 距离最大，此时点位于第二象限．

由， 可求得直线的解析式为： ，

设，PQ在直线上， ，

圆半径为， ，

解之得（舍去）或者，故．

∴的解析式为: ．

将抛物线记为向左平移再向上平移即可得到抛物线记为．