题目内容
16. 如图,己知△ABD,△BCE,△ACF都是等边三角形.
如图,己知△ABD,△BCE,△ACF都是等边三角形.求证:四边形ADEF是平行四边形.
分析 根据△ABD与△BCE是等边三角形,利用边角边定理容易得到全等条件证明△ABC≌△DBE,然后利用全等三角形对应边相等的性质得到DE=AC,又因为△ACF也是等边三角形,根据等边三角形的三条边都相等的性质,AC=AF,所以DE=AF,同理可证AD=EF,然后根据两组对边相等的四边形是平行四边形即可证明;
解答 证明:∵△ABD和△BCE都是等边三角形,
∴∠DBE+∠EBA=∠ABC+∠EBA=60°,
∴∠DBE=∠ABC,
在△ABC与△DBE中,
$\left\{\begin{array}{l}{BD=BA}\\{∠DBE=∠ABC}\\{BE=BC}\end{array}\right.$,
∴△ABC≌△DBE(SAS)
∴AC=DE,
又∵△ACF是等边三角形,
∴AF=AC,
∴DE=AF,
同理可得:EF=AD,
∴四边形ADEF平行四边形;
点评 本题主要考查了等边三角形的性质,全等三角形的判定与性质,平行四边形的判定,菱形的判定,是小综合题,但难度不大.

练习册系列答案
相关题目
9.当前,“低头族”已成为热门话题之一,小颖为了了解路边行人边走路边低头看手机的情况,她应采用的收集数据的方式是( )
| A. | 对学校的同学发放问卷进行调查 | |
| B. | 对在路边行走的学生随机发放问卷进行调查 | |
| C. | 对在图书馆里看书的人发放问卷进行调查 | |
| D. | 对在路边行走的路人随机发放问卷进行调查 |
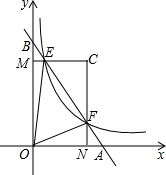 如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于A,B与反比例函数y=$\frac{k}{x}$(k>0且为常数)在第一象限的图象交于点E,F,过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C,若$\frac{BE}{BF}$=$\frac{2}{5}$,则$\frac{{S}_{△CEF}}{{S}_{△OEF}}$=$\frac{3}{7}$.
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于A,B与反比例函数y=$\frac{k}{x}$(k>0且为常数)在第一象限的图象交于点E,F,过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C,若$\frac{BE}{BF}$=$\frac{2}{5}$,则$\frac{{S}_{△CEF}}{{S}_{△OEF}}$=$\frac{3}{7}$.