题目内容

10．一个n边形的每个内角都相等，且它的每一个外角与相邻的内角度数之比为1：2，试求这个n边形的边数．

分析 先根据多边形的内角和外角的关系，求出一个外角．再根据外角和是固定的360°，从而可代入公式求解．

解答 解：设多边形的一个外角为x度，则一个内角为2x度，依题意得
x+2x=180，
解得x=60．
360÷60=6．
故这个n边形的边数为6．

点评 本题考查多边形的内角与外角关系、方程的思想．关键是记住多边形的每一个内角与其相邻的外角互补、及外角和的特征．

练习册系列答案
相关题目
20．如图，过⊙O上一点C作弦BA的垂线，交BA延长线于D点，连OA、CA，若AC平分∠OAD．
（1）求证：CD为⊙O的切线；
（2）若圆的半径为5，CD=4，求AD的长．
1．用代数式表示：
（1）已知正方形的面积为5x，求正方形的边长；
（2）已知△ABC的面积为49S，底边BC上的高是底边BC长的14倍，求BC的长．
18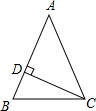．如图，等腰三角形ABC中，AB=AC，∠A=50°，CD⊥AB于D，则∠DCB等于（　　）
A．40°B．30°C．23°D．25°
5．计算：
（1）-24-6÷（-2）×|-$\frac{1}{3}$|；
（2）-32×2+33×3+48÷（-2）×（-1）2015．
15．如果抛物线y=ax2+bx+c，过定点M（1，1），则称此抛物线为定点抛物线．
（1）请你写出一条定点抛物线的一个解析式为y=x2-2x+2．
（2）已知定点抛物线y=-x2+2bx+c+1，求该抛物线顶点纵坐标的值最小时的解析式．
2．营口市某楼盘准备以每平方米4000均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望．为了加快资金周转，房地产开发商对价格经过两次下调后，决定以每平方米3240元的均价开盘销售．
（1）求平均每次下调的百分率；
（2）某人准备以开盘均价购买一套100平方米的房子，开发商还给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，送两年物业管理费，物业管理费是每平方米每月1.5元，请问哪种方案更优惠？
7．三角形的外心具有的性质是（　　）
A．到三边的距离相等B．外心一定在三角形外
C．到三个顶点的距离相等D．外心一定在三角形内
8．计算：
（1）$\frac{{{a^2}-81}}{{{a^2}+6a+9}}÷\frac{9-a}{2a+6}•\frac{a+3}{a+9}$
（2）（$\frac{1}{m}$+$\frac{1}{n}$）÷$\frac{m+n}{n}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网