题目内容
 如图,A,B,C,D在同一直线,AB=CD,DE∥AF,要使△ACF≌△DBE,则边BE与CF应满足的条件是
如图,A,B,C,D在同一直线,AB=CD,DE∥AF,要使△ACF≌△DBE,则边BE与CF应满足的条件是考点:全等三角形的判定
专题:开放型
分析:根据平行线的性质得出∴∠A=∠D,∠EBD=∠FCA,求出AC=BD,根据全等三角形的判定得出即可.
解答:解:BE∥CF,
理由是:∵BE∥CF,DE∥AF,
∴∠A=∠D,∠EBD=∠FCA,
∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
在△ACF和△DBE中
∴△ACF≌△DBE,
故答案为:BE∥CF.
理由是:∵BE∥CF,DE∥AF,
∴∠A=∠D,∠EBD=∠FCA,
∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
在△ACF和△DBE中
|
∴△ACF≌△DBE,
故答案为:BE∥CF.
点评:本题考查了平行线的性质和全等三角形的判定的应用,主要考查学生运用定理进行推理的能力,题目比较好,难度适中.

练习册系列答案
相关题目
下列汽车图标中,中心对称图形是( )
A、 |
B、 |
C、 |
D、 |
 如图,直线a、b、c、d,已知c⊥a,c⊥b,直线b、c、d交于一点,若∠1=60°,则∠2等于
如图,直线a、b、c、d,已知c⊥a,c⊥b,直线b、c、d交于一点,若∠1=60°,则∠2等于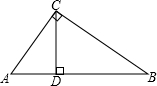 如图,在Rt△ABC中,∠C=90°,AC=6、BC=8,CD⊥AB,则CD=
如图,在Rt△ABC中,∠C=90°,AC=6、BC=8,CD⊥AB,则CD=