题目内容
6.如图,直线AB与两坐标轴分别相交于A、B两点,A(4,0),B(0,4),点M是线段AB上任意一点(A、B点除外)过M分别作MC⊥OA于点C,MD⊥OB于D.(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化,并说明理由.
(2)设MC=x,用含x的代数式表示长方形OCMD的面积,并求出当点M运动到什么位置时,长方形OCMD的面积有最大值?最大值是多少?
(3)当长方形OCMD为正方形时,将正方形OCMD沿着x轴的正方向移动,设平移的距离为a(0<a<4),在平移过程中正方形OCMD始终被线段AB分割成两个图形.当a为何值时正方形OCMD被线段分割形成的三角形的面积是1?
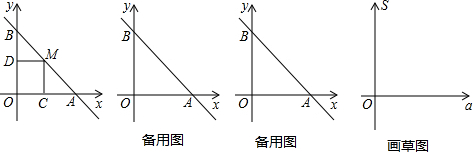
分析 (1)设点M的横坐标为x,则点M的纵坐标为-x+4(0<x<4,x>0,-x+4>0)用坐标表示线段的长度则:MC=|-x+4|=-x+4,MD=|x|=x,根据四边形的周长计算方法计算即可发现,当点M在AB上运动时,四边形OCMD的周长不发生变化,总是等于8.
(2)先用x表示四边形的面积S四边形OCMD=-(x-2)2+4,再利用四边形OCMD的面积是关于点M的横坐标x(0<x<4)的二次函数,并且x=2,可知即当点M运动到线段AB的中点时,四边形OCMD的面积最大且最大面积为4.
(3)分两种情况进行讨论,当0<a≤2时,$\frac{1}{2}$a2=1;当2<a≤4时,$\frac{1}{2}(4-a)^{2}=1$,求出a的值,即可解答.
解答 解:(1)设点M的横坐标为x,则点M的纵坐标为-x+4(0<x<4,-x+4>0),
则:MC=|-x+4|=-x+4,MD=|x|=x,
∴C四边形OCMD=2(MC+MD)=2(-x+4+x)=8,
∴当点M在AB上运动时,四边形OCMD的周长不发生变化,总是等于8.
(2)根据题意得:S四边形OCMD=MC•MD=(-x+4)•x=-x2+4x=-(x-2)2+4,
∴四边形OCMD的面积是关于点M的横坐标x(0<x<4)的二次函数,并且当x=2,S有最大值4,
此时M是AB的中点,
即当点M运动到线段AB的中点时,四边形OCMD的面积最大且最大面积为4.
(3)①当0<a≤2时,如图(2),
MH=a,
∵A(4,0),B(0,4),
∴OA=OB=4,
∴∠OAB=∠OBA=45°,
∴∠CKA=45°,
∵∠MKH=∠CKA,
∴∠MKH=∠OAB=45°,
∴MK=NH=a,
∴$\frac{1}{2}$a2=1,
∴a=±$\sqrt{2}$,
a=-$\sqrt{2}$(舍去),
∴a=$\sqrt{2}$;
②如图(3),
当2<a≤4时,OO′=a,O′A=4-a,
∵∠OAB=45°,
∴∠O′HA=45°,
∴OH=O′A=4-a,
∴$\frac{1}{2}(4-a)^{2}=1$,
解得:a=4±$\sqrt{2}$,
经检验a=4$+\sqrt{2}$>4,不合题意,舍去,
∴a=4-$\sqrt{2}$,
综上所述,当a=$\sqrt{2}$或a=4-$\sqrt{2}$时,正方形OCMD被线段分割形成的三角形的面积是1.
点评 本题结合四边形的性质考查二次函数的综合应用,有关函数和几何图形的综合题目,要利用几何图形的性质和二次函数的性质把数与形有机地结合在一起,利用题中所给出的面积和周长之间的数量关系求解是本题的关键.

| A. | 2:3:2:3 | B. | 1:1:4:4 | C. | 1:2:3:4 | D. | 3:4:4:3 |
 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.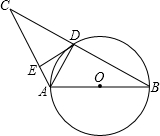 已知如图,AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
已知如图,AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.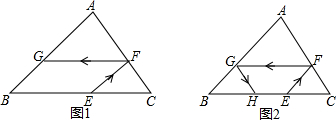
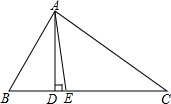 如图,在△ABC中,∠B>∠C,AD⊥BC,AE平分∠BAC,
如图,在△ABC中,∠B>∠C,AD⊥BC,AE平分∠BAC, 如图是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )
如图是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )